
����Ŀ�����磬��ƽ��ֱ������ϵ�У���![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() ��
��![]() ���ϣ���ֱ��
���ϣ���ֱ��![]() .��
.��![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�
�ĶԳƵ�![]() �պ���
�պ���![]() ���ϣ�����
���ϣ�����![]() .
.
��1��д��һ��![]() �����꣬�����ֱ��
�����꣬�����ֱ��![]() ��Ӧ�ĺ�������ʽ��
��Ӧ�ĺ�������ʽ��
��2����![]() ���߶�
���߶�![]() �ϣ�����
�ϣ�����![]() ��
��![]() ��
��![]() ����
����![]() �ǵ���ֱ��������ʱ�����
�ǵ���ֱ��������ʱ�����![]() ���ꣻ
���ꣻ
��3����ͼ�ڣ��ڣ�2���������£���![]() �ӵ�
�ӵ�![]() ������ÿ��2����λ���ȵ��ٶ���ԭ��
������ÿ��2����λ���ȵ��ٶ���ԭ��![]() �˶��������
�˶��������![]() ʱֹͣ�˶�������
ʱֹͣ�˶�������![]() ����
����![]() ��
��![]() �Ĵ��ߣ���
�Ĵ��ߣ���![]() ���ڵ�
���ڵ�![]() ���ʵ�
���ʵ�![]() �˶�����ʱ
�˶�����ʱ![]() �ǵ���������.
�ǵ���������.
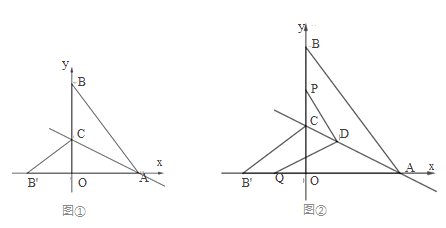
���𰸡���1��![]() ��
��![]() ��2����
��2����![]() ����Ϊ
����Ϊ![]() ����3����
����3����![]() �˶�ʱ��Ϊ1���
�˶�ʱ��Ϊ1���![]() ���3.75��.
���3.75��.
��������
��1���ɹ��ɶ������AB=10���������A![]() =10���Ӷ������
=10���Ӷ������![]() ����C��0��m������ֱ��������
����C��0��m������ֱ��������![]() �У����ù��ɶ��������m��ֵ���Ӷ�ȷ����C�����꣬�����ô���ϵ�������AC�Ľ���ʽ���ɣ�
�У����ù��ɶ��������m��ֵ���Ӷ�ȷ����C�����꣬�����ô���ϵ�������AC�Ľ���ʽ���ɣ�
��2����![]() ��ֱƽ��
��ֱƽ��![]() ��֤
��֤![]() ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ��֤��
��֤��![]() �ɵ�DE=DF����D��a��a������
�ɵ�DE=DF����D��a��a������![]() ��⼴�ɣ�
��⼴�ɣ�
��3��������������ٵ�![]() ʱ���ڵ�
ʱ���ڵ�![]() ʱ���۵�
ʱ���۵�![]() ʱ���������ۼ��ɵý⣺
ʱ���������ۼ��ɵý⣺
��1��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��![]() ����ֱ��
����ֱ��![]() �ĶԳƣ�
�ĶԳƣ�
![]() ��ֱƽ��
��ֱƽ��![]() ��
��
![]() ��
��
![]() ��
��
���![]() ����Ϊ
����Ϊ![]() ����
����![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��
![]()
![]() ��
��
![]() ��
��![]() ����Ϊ
����Ϊ![]() .
.
![]() ��ֱ��
��ֱ��![]() ��Ӧ�ĺ�������ʽΪ
��Ӧ�ĺ�������ʽΪ![]() ��
��
��![]() ���룬
���룬
��![]() ��
��
���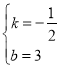 ��
��
![]() ֱ��
ֱ��![]() ��Ӧ�ĺ�����ϵ��Ϊ
��Ӧ�ĺ�����ϵ��Ϊ![]() ��
��
��2��![]() ��ֱƽ��
��ֱƽ��![]() ��
��
![]() ��
��
![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
![]()
����![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ���ڵ�
���ڵ�![]() .
.
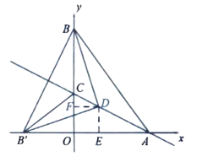
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ���
���![]() ����Ϊ
����Ϊ![]() ��
��
�ѵ�![]() ����
����![]() ��
��
��![]()
![]() ��
��
![]() ��
��![]() ����Ϊ
����Ϊ![]() ��
��
��3��ͬ��2���ɵ�![]()
��![]()
![]()
![]()
�ٵ�![]() ʱ��
ʱ��
![]() �ᣬ
�ᣬ
![]()
![]()
![]()
![]() ��
��![]() �˶�ʱ��Ϊ1��.
�˶�ʱ��Ϊ1��.
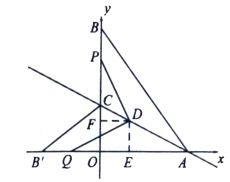
�ڵ�![]() ʱ��
ʱ��
![]()
![]()
![]() ��
��
![]()
![]()
![]() ��
��![]() �˶�ʱ��Ϊ
�˶�ʱ��Ϊ![]() ��.
��.
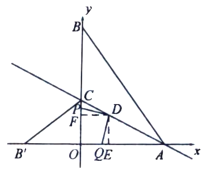
�۵�![]() ʱ��
ʱ��
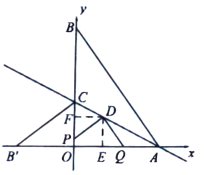
��![]() ����
����![]()
![]() ��
��![]() ��
��![]() ��
��
![]()
![]()
![]()
![]()
![]() ��
��![]() �˶�ʱ��Ϊ3.75��.
�˶�ʱ��Ϊ3.75��.
������������![]() �˶�ʱ��Ϊ1���
�˶�ʱ��Ϊ1���![]() ���3.75��.
���3.75��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵȱ�![]() �У���
����![]() �DZ�
�DZ�![]() ��һ��.������
��һ��.������![]() ����
����![]() ��������
��������![]() �ĶԳƵ�Ϊ��
�ĶԳƵ�Ϊ��![]() .����
.����![]() ���ӳ���������
���ӳ���������![]() �ڵ�
�ڵ�![]() .
.
��1����ͼ������![]() ��
��
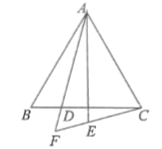
��![]() ��
��![]() ��������ϵ��__________��
��������ϵ��__________��
����![]() ����
����![]() ��ʾ
��ʾ![]() �Ĵ�С��
�Ĵ�С��
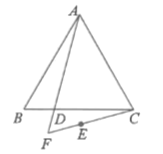
��2����ͼ���õ�ʽ��ʾ�߶�![]() ��
��![]() ��
��![]() ֮���������ϵ����֤��.
֮���������ϵ����֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
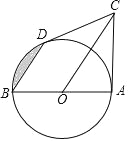
����Ŀ����ͼ��AB�ǡ�O��ֱ����CD�С�O�ڵ�D����BD��OC������AC��
��1����֤��AC�ǡ�O�����ߣ�
��2����AB=OC=4����ͼ����Ӱ���ֵ����������������ź��У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
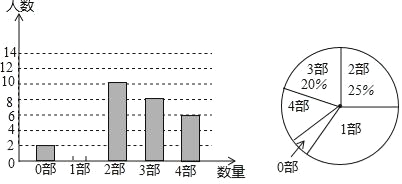
����Ŀ���л��Ļ���ԴԶ����������ѧ���棬�����μǡ������������塷����ˮ䰴���������¥�Ρ����ҹ��Ŵ���ƪС˵�еĵ��ʹ���������Ϊ���Ĵ��ŵ���������ij��ѧΪ���˽�ѧ�����Ĵ�ŵ��������Ķ�������͡��Ĵ�ŵ�����������˼�������������ȫУѧ���н����˳������飬���ݵ��������Ƴ���ͼ��ʾ��������������ͳ��ͼ������ͼ����Ϣ����������⣺
��1�����ε������� ����ѧ��������ͳ��ͼ�С�1�����������ε�Բ�Ľ�Ϊ�� ���ȣ�����ȫ����ͳ��ͼ��
��2������ѧ����1600��ѧ����ͨ������Ԥ������4���������˵�ѧ��������
��3��û�ж����Ĵ�ŵ�����������ѧ�������Ĵ�̶������и������ѡ��һ�����Ķ���������ѡ��ͬһ�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10�֣���ͼ��AB����O��ֱ����OD����BC�ڵ�F������O�ڵ�E������CE��AE��CD������AEC=��ODC��
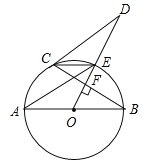
��1����֤��ֱ��CDΪ��O�����ߣ�
��2����AB=5��BC=4�����߶�CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ⶳ�Ρ���üɽ������ɫС�ԣ���Ʒ����ʡ���⣬����һ����Ʒ���۵��ھ���ʱ���֣����ÿ���Ʒӯ��10Ԫ��ÿ����۳�50�䣻��ÿ���Ʒ�Ǽ�1Ԫ����������������2�䣮
��1���ָ����۵�ÿ��ӯ��600Ԫ��ͬʱ��Ҫ�˿͵õ�ʵ�ݣ���ôÿ���ƷӦ�Ǽ۶���Ԫ��
��2���������۵㵥���Ӿ��ýǶȿ��ǣ�ÿ���ƷӦ�Ǽ۶���Ԫ���ܻ�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���֪�߶�a��PΪ�߶�a������һ�㣬��֪ͼ��M��QΪͼ��M������һ�㣬��P��Q�����ľ�����Сʱ������ʱPQ�ij��ȳ�Ϊͼ��M���߶�a�Ľ���ࣻ��P��Q�����ľ������ʱ������ʱPQ�ij��ȳ�Ϊͼ��M���߶�a��Զ��࣮

�����Ķ����Ͻ���������⣺
��ͼ1����ƽ��ֱ������ϵxOy�У���A������Ϊ����2����2����������ABCD�ĶԳ�����Ϊԭ��O��
��1���߶�AB���߶�CD�Ľ�������� ����Զ������� ����
��2����ͼ2��ֱ��y����x+6��x�ᣬy��ֱ��ڵ�E��F�����߶�EF��������ABCD�Ľ�������� ����Զ������� ����
��3��ֱ��y��x+b��b��0����x�ᣬy��ֱ��ڵ�R��S���߶�RS��������ABCD�Ľ������![]() ����b��ֵ���� ����
����b��ֵ���� ����
��4����ƽ��ֱ������ϵxOy�У���һ������GHMN�����˾���������һ����������OΪԲ��1Ϊ�뾶��Բ�ϣ�������������Բ�ϻ�Բ�ڣ���������ABCD�Ƶ�O��תһ�ܣ�����ת�����У��������GHMN�Ľ�������Сֵ���� ��Զ�������ֵ���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
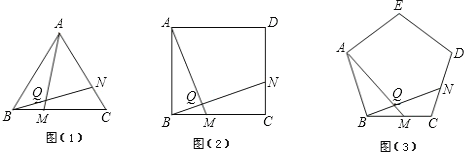
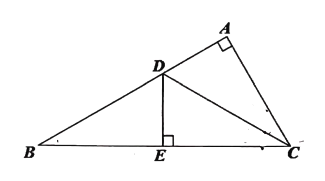
����Ŀ����1����ͼ��1������֪��ABCΪ�������Σ���M��BC��һ�㣬��N��AC��һ�㣬AM��BN�ཻ�ڵ�Q��BM=CN�������BQM�Ķ�����
��2������1���е�������ABC���ֱ��Ϊ������ABCD���������ABCDE������n����ABCD��������N��AC��һ������Ϊ��N��CD��һ�㣬�����������䣬�ֱ��ƶϳ���BQM���ڶ��ٶȣ������������±���
������� | ������ | ������� | ���� | ��n���� |
��BQM�Ķ��� |
|
| ���� |
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ƽ��
ƽ��![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() .
.
��1����֤��![]() ��
��![]() ��
��
��2����![]() ����
����![]() �Ķ���.
�Ķ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com