
【题目】如图,已知矩形 OABC,以点 O 为坐标原点建立平面直角坐标系,其中 A(2,0), C(0,3),点 P 以每秒 1 个单位的速度从点 C 出发在射线 CO 上运动,连接 BP,作 BE⊥PB 交 x 轴于点 E,连接 PE 交 AB 于点 F,设运动时间为 t 秒.
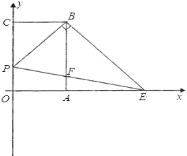
(1)当 t=2 时,求点 E 的坐标;
(2)在运动的过程中,是否存在以 P、O、E 为顶点的三角形与△PCB 相似.若存在,请求出点 P 的坐标;若不存在,请说明理由.
【答案】(1)(5,0);(2)存在.
【解析】
(1)本题需先求出AB=AE,再求出DE=5,即可求出点E的坐标.
(2)本题需先求出CP=CB=2,即可求出t的值.(3)本题需先证出△BCP~△BAE,求出
AE= t,再证出△POE~△PCB,求出的t值,再求出OP的长,即可求出P的坐标.
解:(1)当 t=2 时,PC=2,∵BC=2,∴PC=BC,∴∠PBC=45°,∴∠BAE=90°,
∴∠AEB=45°,∴AB=AE=3,OE=5,∴点 E 的坐标是(5,0);
(2)存在,
∵∠ABE+∠ABP=90°
∠PBC+∠ABP=90°
∴∠ABE=∠PBC
∵∠BAE=∠BCP=90°
∴△POE![]() △BAE
△BAE
∴![]() =
=![]()
∴![]() =
=![]()
∴AE=![]() t
t
∵若△POE![]() △PCB
△PCB
∴![]()
∴![]() =
=![]()
![]() ,
,![]() (舍去)
(舍去)
∴P的坐标为(0,![]() ).
).


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】如图①,一个长为![]() ,宽为
,宽为![]() 的长方形,沿途中的虚线用剪刀均匀的分成四个小长方形,然后按图②的形状拼成一个正方形.
的长方形,沿途中的虚线用剪刀均匀的分成四个小长方形,然后按图②的形状拼成一个正方形.
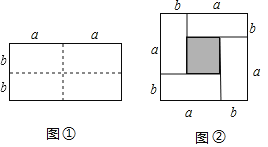
(1)观察图②,请用两种不同的方法求图②中阴影部分的面积.
方法1:________________________________________(只列式,不化简)
方法2:________________________________________(只列式,不化简)
(2)请写出![]() 三个式子之间的等量关系:_______________________________.
三个式子之间的等量关系:_______________________________.
(3)根据(2)题中的等量关系,解决如下问题:若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在长方形ABCD中,AB=12cm,BC=10cm,点P从A出发,沿A→B→C→D的路线运动,到D停止;点Q从D点出发,沿D→C→B→A路线运动,到A点停止.若P、Q两点同时出发,速度分别为每秒lcm、2cm,a秒时P、Q两点同时改变速度,分别变为每秒2cm、![]() cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
(1)求出a值;
(2)设点P已行的路程为y1(cm),点Q还剩的路程为y2(cm),请分别求出改变速度后,y1、y2和运动时间x(秒)的关系式;
(3)求P、Q两点都在BC边上,x为何值时P、Q两点相距3cm?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 。
。
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5。当△ABC是等腰三角形时,求k的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
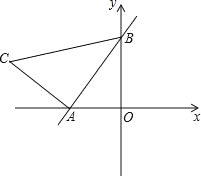
【题目】如图,直线y=kx+2与x轴、y轴分别交于A、B两点,OA:OB=![]() .以线段AB为边在第二象限内作等腰Rt△ABC,∠BAC=90°.
.以线段AB为边在第二象限内作等腰Rt△ABC,∠BAC=90°.
(1)求点A的坐标和k的值;
(2)求点C坐标;
(3)直线y=![]() x在第一象限内的图象上是否存在点P,使得△ABP的面积与△ABC的面积相等?如果存在,求出点P坐标;如果不存在,请说明理由.
x在第一象限内的图象上是否存在点P,使得△ABP的面积与△ABC的面积相等?如果存在,求出点P坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一张三角形纸片![]() 如图甲
如图甲![]() ,其中
,其中![]() 将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为
将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为![]() 如图乙
如图乙![]() 再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为
再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为![]() 如图丙
如图丙![]() 原三角形纸片ABC中,
原三角形纸片ABC中,![]() 的大小为______
的大小为______![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
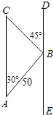
【题目】一架外国侦察机沿![]() 方向侵入我国领空进行非法侦察,我空军的战斗机沿
方向侵入我国领空进行非法侦察,我空军的战斗机沿![]() 方向与外国侦察机平行飞行,进行跟踪监视,我机在
方向与外国侦察机平行飞行,进行跟踪监视,我机在![]() 处与外国侦察机
处与外国侦察机![]() 处的距离为
处的距离为![]() 米,
米,![]() 为
为![]() ,这时外国侦察机突然转向,以偏左
,这时外国侦察机突然转向,以偏左![]() 的方向飞行,我机继续沿
的方向飞行,我机继续沿![]() 方向以
方向以![]() 米/秒的速度飞行,外国侦察机在
米/秒的速度飞行,外国侦察机在![]() 点故意撞击我战斗机,使我战斗机受损.问外国侦察机由
点故意撞击我战斗机,使我战斗机受损.问外国侦察机由![]() 到
到![]() 的速度是多少?(结果保留整数,参考数据
的速度是多少?(结果保留整数,参考数据![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与直线都经过坐标轴的正半轴上A(4,0),B两点,该抛物线的对称轴x=﹣1,与x轴交于点C,且∠ABC=90°,求:
(1)直线AB的解析式;
(2)抛物线的解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com