练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
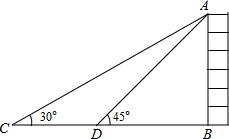
    7．如图，某校数学兴趣小组在大厦前的平地上C处，测得大厦顶端A的仰角∠ACB=30°，在D处测得大厦顶端A的仰角∠ADB=45°，那么从点A观察C、D处的视角∠CAD的度数为（　　）
    A．60°B．45°C．30°D．15°

    分析 由某校数学兴趣小组在大厦前的平地上C处，测得大厦顶端A的仰角∠ACB=30°，在D处测得大厦顶端A的仰角∠ADB=45°，利用三角形外角的性质，即可求得答案．

    解答 解：∵∠ACB=30°，∠ADB=45°，
    ∴∠CAD=∠ADB-∠ACB=15°．
    故选D．

    点评 此题考查了仰角的定义以及三角形外角的性质．注意由图得到∠ADB是△ACD的外角是解此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

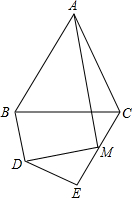    17．在△ABC中，AB=AC，∠ABC=α，在四边形BDEC中，DB=DE，∠BDE=2α，M为EC的中点，
    （1）求证：AM⊥DM（两种做法）
    （2）当α等于多少度时，AM=DM？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．解方程
    （1）（x+1）（x-2）=x+1；                 
    （2）3x2-x-1=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如图，点A是菱形ABCD的对角线BE的延长线上一点，则图中的全等三角形有（　　）对．
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

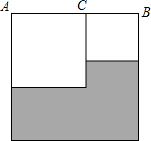    2．如图，已知线段AB=10cm，点C在线段AB上，分别以AC、BC、AB为边向下作正方形．
    （1）当阴影部分的面积为42cm2时，请求出AC的长；
    （2）阴影部分的面积能否为60cm2？如果能，请求出AC的长；如果不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，△ABE≌△ACD，点B、D、E、C在一条直线上．
    （1）∠BAD与∠CAE有何关系？请说明理由．
    （2）BD与CE相等吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．计算：
    （1）20-（-7）-|-2|
    （2）（$\frac{1}{3}$-$\frac{5}{9}$+$\frac{11}{12}$）×（-36）
    （3）-14-（2-3）2×（-2）3
    （4）-2×（-$\frac{1}{2}$）+8÷（-2）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．一定为一元二次方程的是（　　）
    A．x2+$\frac{3}{x}$-2=0B．ax2-bx+c=0C．（x+2）（x-5）=x2D．3x2=-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．若m、n是方程x2+2012x-1=0的两个实数根，则m2n+mn2-mn的值是2013．

    查看答案和解析>>

    同步练习册答案