
【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0),C(3,0),D(3,4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,沿线段AB向点B运动.同时动点Q从点C出发,沿线段CD向点D运动.点P,Q的运动速度均为每秒1个单位.运动时间为t秒.过点P作PE⊥AB交AC于点E.
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)过点E作EF⊥AD于F,交抛物线于点G,当t为何值时,△ACG的面积最大?最大值为多少?
(3)在动点P,Q运动的过程中,当t为何值时,在矩形ABCD内(包括边界)存在点H,使以C,Q,E,H为顶点的四边形为菱形?请直接写出t的值.
【答案】
(1)解:A(1,4).
由题意知,可设抛物线解析式为y=a(x﹣1)2+4
∵抛物线过点C(3,0),
∴0=a(3﹣1)2+4,
解得,a=﹣1,
∴抛物线的解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3
(2)解:∵A(1,4),C(3,0),
∴可求直线AC的解析式为y=﹣2x+6.
∵点P(1,4﹣t).
∴将y=4﹣t代入y=﹣2x+6中,解得点E的横坐标为x=1+ ![]() .
.
∴点G的横坐标为1+ ![]() ,代入抛物线的解析式中,可求点G的纵坐标为4﹣
,代入抛物线的解析式中,可求点G的纵坐标为4﹣ ![]() .
.
∴GE=(4﹣ ![]() )﹣(4﹣t)=t﹣
)﹣(4﹣t)=t﹣ ![]() .
.
又∵点A到GE的距离为 ![]() ,C到GE的距离为2﹣
,C到GE的距离为2﹣ ![]() ,
,
即S△ACG=S△AEG+S△CEG= ![]() EG
EG ![]() +
+ ![]() EG(2﹣
EG(2﹣ ![]() )
)
= ![]() 2(t﹣
2(t﹣ ![]() )=﹣
)=﹣ ![]() (t﹣2)2+1.
(t﹣2)2+1.
当t=2时,S△ACG的最大值为1
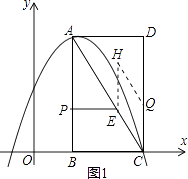
(3)解:第一种情况如图1所示,点H在AC的上方,由四边形CQEH是菱形知CQ=CE=t,
根据△APE∽△ABC,知
![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得t=20﹣8
,解得t=20﹣8 ![]() ;
;
第二种情况如图2所示,点H在AC的下方,由四边形CQHE是菱形知CQ=QE=EH=HC=t,PE= ![]() t,EM=2﹣
t,EM=2﹣ ![]() t,MQ=4﹣2t.
t,MQ=4﹣2t.
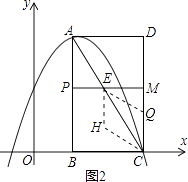
则在直角三角形EMQ中,根据勾股定理知EM2+MQ2=EQ2,即(2﹣ ![]() t)2+(4﹣2t)2=t2,
t)2+(4﹣2t)2=t2,
解得,t1= ![]() ,t2=4(不合题意,舍去).
,t2=4(不合题意,舍去).
综上所述,t=20﹣8 ![]() 或t=
或t= ![]() .
.
【解析】(1)顶点A坐标可根据A、B横坐标相同,与D的纵坐标关相同求出,利用待定系数法求出解析式;(2)通过竖直线段把三角形分割为两个三角形,用t的代数式表示S△ACG,构建函数,利用配方法求出最值;(3)以C,Q,E,H为顶点的四边形为菱形可分类讨论为:四边形CQEH是菱形;四边形CQHE是菱形,根据菱形的性质、相似三角形性质及勾股定理可求出.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD=110°,将四边形BCD绕点A逆时针旋转到平行四边形AB′C′D′的位置,旋转角α(0°<α<70°),若C′D′恰好经过点D,则α的度数为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图1,直线![]() 、
、![]() 、
、![]() 两两相交,交点分别为点A、B、C,点D在线段
两两相交,交点分别为点A、B、C,点D在线段![]() 上,过点D作
上,过点D作![]() 交
交![]() 于点E,过点E作
于点E,过点E作![]() 交
交![]() 于点F.若
于点F.若![]() ,求
,求![]() 的度数.请将下面的解答过程补充完整,并填空
的度数.请将下面的解答过程补充完整,并填空
解:∵![]() ,∴
,∴![]() ________.( )
________.( )
∵![]() ,∴________
,∴________![]() ( )
( )
∴![]() .(等量代换)
.(等量代换)
∵![]() ,∴
,∴![]() ________°.
________°.
应用:如图2,直线![]() 、
、![]() 、
、![]() 两两相交,交点分别为点A、B、C,点D在线段
两两相交,交点分别为点A、B、C,点D在线段![]() 的延长线上,过点D作
的延长线上,过点D作![]() 交
交![]() 于点E,过点E作
于点E,过点E作![]() 交
交![]() 于点F.若
于点F.若![]() ,求
,求![]() 的度数,并仿照(1)进行说明.
的度数,并仿照(1)进行说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠ABC=60°,点D是其角平分线上一点,BD=CD=6,DE//AB交BC于点E.若在射线BA上存在点F,使![]() ,请写出相应的BF的长:BF=_________
,请写出相应的BF的长:BF=_________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在面积为3的正方形ABCD中,E,F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.
(1)求证:△ABE≌△BCF;
(2)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(3)现将△ABE绕点A逆时针方向旋转到△AB′E′(如图2),使点E落在CD边上的点E′处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD= ![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,
其中正确的有( )
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.

(1)求该一次函数的解析式;
(2)求点C和点D的坐标;
(3)求△AOB的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将 ![]() 沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC
沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC
(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为 ![]() 的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交
的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交 ![]() 于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com