
 已知△ABC是边长为4的等边三角形,BC在x轴上,点D为BC的中点,点A在第一象限内,AB与y轴的正半轴交与点E,已知点B(-1,0).
已知△ABC是边长为4的等边三角形,BC在x轴上,点D为BC的中点,点A在第一象限内,AB与y轴的正半轴交与点E,已知点B(-1,0).分析 (1)△ABC是边长为4的等边三角形,则BC=4,而点D为BC的中点,BD=2,点B(-1,0),则OD=1,就可以求出A的横坐标,等边三角形的高线长,就是A的纵坐标.在直角三角形OBE中,根据三角函数可以求出OE的长,即得到E点的纵坐标.
(2)已经求出A,E的坐标,根据待定系数法就可以求出函数的解析式.
(3)先作点D关于AC的对称点D',连接BD'交AC于点P,则PB与PD的和取最小值,即△PBD的周长L取最小值.根据三角函数求的D′的坐标,再求出直线BD′的解析式,以及直线AC的解析式,两直线的交点就是P的坐标.把点P的坐标代入二次函数的解析式,就可以判断是否在函数的图象上.
解答 解:(1)连接AD,如图1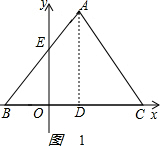 ,
,
∵△ABC是边长为4的等边三角形,又B的坐标为(-1,0),BC在x轴上,A在第一象限,
∴点C在x轴的正半轴上,
∴C的坐标为(3,0),由中点坐标公式,得:D的坐标为(1,0).
显然AD⊥BC且AD=$\sqrt{3}$BD=2$\sqrt{3}$,
∴A的坐标是(1,2$\sqrt{3}$).
OE=$\frac{1}{2}$AD,得E(0,$\sqrt{3}$);
(2)因为抛物线y=-$\frac{6\sqrt{3}}{7}$x2+bx+c过点A、E,
由待定系数法得:c=$\sqrt{3}$,b=$\frac{13\sqrt{3}}{7}$,
抛物线的解析式为y=-$\frac{6\sqrt{3}}{7}$x2+$\frac{13\sqrt{3}}{7}$x+$\sqrt{3}$;
(3)作点D关于AC的对称点D',
连接BD'交AC于点P,则PB与PD的和取最小值,
即△PBD的周长L取最小值,如图2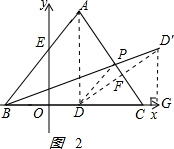 .
.
∵D、D′关于直线AC对称,
∴DD′⊥AC,即∠D′DC=30°,
DF=$\sqrt{3}$,DD'=2$\sqrt{3}$,
求得点D'的坐标为(4,$\sqrt{3}$),
直线BD'的解析式为:y=$\frac{\sqrt{3}}{5}$x+$\frac{\sqrt{3}}{5}$,
直线AC的解析式为:y=-$\sqrt{3}$x+3$\sqrt{3}$,
求直线BD'与AC的交点可,得
点P的坐标($\frac{7}{3}$,$\frac{2\sqrt{3}}{3}$).
此时BD'=$\sqrt{B{G}^{2}+D′{G}^{2}}$=$\sqrt{{5}^{2}+(\sqrt{3})^{2}}$=2$\sqrt{7}$,
所以△PBD的最小周长L为2$\sqrt{7}$+2,
把点P的坐标代入y=-$\frac{6\sqrt{3}}{7}$+$\frac{13\sqrt{3}}{7}$x+$\sqrt{3}$成立,
所以此时点P在抛物线上.
点评 本题主要考查了二次函数综合题,利用待定系数法求函数的解析式,求两条线段的和最小的问题,一般是转化为两点之间线段最短的问题.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在等边△ABC中,AC=4,点D、E、F分别在三边AB、BC、AC上,且AF=1,FD⊥DE,∠DFE=60°,则AD的长为( )
如图,在等边△ABC中,AC=4,点D、E、F分别在三边AB、BC、AC上,且AF=1,FD⊥DE,∠DFE=60°,则AD的长为( )| A. | 0.5 | B. | 1 | C. | 1.5 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知:在△ABC中,AC=BC=4,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D.
如图,已知:在△ABC中,AC=BC=4,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com