
【题目】在△ABC中,∠ACB=90°,∠A<45°,点O为AB中点,一个足够大的三角板的直角顶点与点O重合,一边OE经过点C,另一边OD与AC交于点M.
(1)如图1,当∠A=30°时,求证:MC2=AM2+BC2;
(2)如图2,当∠A≠30°时,(1)中的结论是否成立?如果成立,请说明理由;如果不成立,请写出你认为正确的结论,并说明理由;
(3)将三角形ODE绕点O旋转,若直线OD与直线AC相交于点M,直线OE与直线BC相交于点N,连接MN,则MN2=AM2+BN2成立吗?答: (填“成立”或“不成立”)

【答案】(1)、证明过程见解析;(2)、理由见解析;(3)、成立.
【解析】
试题分析:(1)、根据点O为中点,∠ACB=90°得出OA=OB=OC,根据∠A=30°可得∠B=∠COB=60°,根据∠COM=90°得出∠AOM=∠A=30°,则AM=OM,根据Rt△COM的勾股定理得出所求的答案;(2)、过A作AF‖BC交CO的延长线于点F,连接FM,证明△BOC≌△AOF,得出BC=AF,FO=CO,根据Rt△AMF的勾股定理进行说明.
试题解析:(1)、∵O为AB中点,∠ACB=90°∴OA=OB=OC,∵∠A=30°∴∠B=60°
∴∠COB=60° ∵∠COM=90°∴∠AOM=∠A=30°∴AM=OM
在Rt△COM中,由勾股定理得MC2=OM2+OC2∴ MC2=AM2+BC2;
(2)、成立。如图,
 过A作AF‖BC交CO的延长线于点F,连接FM
过A作AF‖BC交CO的延长线于点F,连接FM
∵O为AB中点,可证△BOC≌△AOF,∴BC=AF,FO=CO ∵AF‖BC,∠ACB=90°∴∠CAF=90°
∵FO=CO,∠MOC=90°,∴OM是CF的垂直平分线,∴CM=MF,
在Rt△AMF中,由勾股定理得:MF2=AM2+AF2=AM2+BC2, 即MC2=AM2+BC2
(3)、成立。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,a∥b,直线a,b被直线c所截,AC1 , BC1分别平分∠EAB,∠FBA,AC2 , BC2分别平分∠EAC1 , ∠FBC1;AC3 , BC3分别平分∠EAC2 , ∠FBC2交于点C3…依次规律,得点Cn , 则∠C3=度,∠Cn=度. 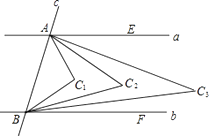
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB=6cm,C是AB的中点,D是AC的中点,则DB等于( )
A. 1.5cm B. 4.5 cm C. 3 cm D. 3.5 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形属于因式分解的是( )
A. (x+2)(x﹣2)=x2﹣4 B. x2﹣2x+3=(x﹣1)2+2
C. x2﹣6xy+9y2=(x﹣3y)2 D. 3(5﹣x)=﹣3(x﹣5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将矩形ABCD沿DE折叠,使顶点A落在DC上的点A′处,然后将矩形展平,沿EF折叠,使顶点A落在折痕DE上的点G处.再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处.如图2.

(1)求证:EG=CH;
(2)已知AF=![]() ,求AD和AB的长.
,求AD和AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
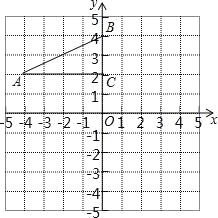
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣4,2)、B(0,4)、C(0,2),
(1)画出△ABC关于点C成中心对称的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)△A1B1C和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com