
| A | B | C | D | E | 平均分 | 方差 | |
| 数学 | 71 | 72 | 69 | 68 | 70 | 70 | 2 |
| 英语 | 88 | 82 | 94 | 85 | 76 | 85 | 36 |
分析 (1)由平均数的概念计算平均数,再根据方差的定义得出即可;
(2)根据标准分的计算公式:标准分=(个人成绩一平均成绩)÷成绩标准差,计算数学和英语的标准分,然后比较.
解答 解:(1)数学成绩的平均分为:$\frac{71+72+69+68+70}{5}=70$;
英语成绩的标准差为:$\frac{1}{5}$[(88-85)2+(82-85)2+(94-85)2+(85-85)2+(76-85)2]=36;
故答案为:70,36;
(2)A同学数学标准分为:$\frac{71-70}{{\sqrt{2}}}=\frac{{\sqrt{2}}}{2}$,
A同学英语标准分为:$\frac{88-85}{6}=\frac{1}{2}$,
因为$\frac{{\sqrt{2}}}{2}$>$\frac{1}{2}$,所以,A同学在本次考试中,数学学科考得更好.
点评 本题考查了平均数和方差的计算,正确把握方差的定义是解题关键.


科目:初中数学 来源: 题型:解答题
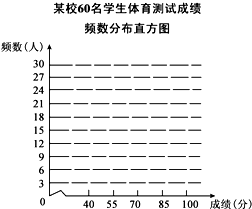 某校为了更好的开展“学校特色体育教育”,从全校八年级的各班分别随机抽取了5名男生和5名女生,组成了一个容量为60的样本,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
某校为了更好的开展“学校特色体育教育”,从全校八年级的各班分别随机抽取了5名男生和5名女生,组成了一个容量为60的样本,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表| 成绩 | 划记 | 频数 | 百分比 |
| 优秀 | 正正正 | a | 30% |
| 良好 | 正正正正正正 | 30 | b |
| 合格 | 正 | 9 | 15% |
| 不合格 |  | 3 | 5% |
| 合计 | 60 | 60 | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
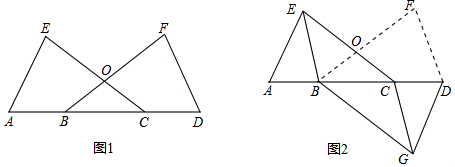
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1)(3) | B. | (1)(4) | C. | (1)(3)(4) | D. | (2)(3)(4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com