
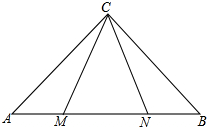
 在Rt△ABC中,AC=BC,∠ACB=90°,∠MCN=45°
在Rt△ABC中,AC=BC,∠ACB=90°,∠MCN=45°分析 (1)作AF⊥AB,使AF=BE,连接DF,根据SAS证得△CAF≌△CBE和△CDF≌△CDE,再由勾股定理和等量代换即可解答;
(2)作AF⊥AB,使AF=BE,连接DF,根据SAS证得△CAF≌△CBE和△CDF≌△CDE,再由勾股定理和等量代换即可解答.
解答 (1)证明:如图,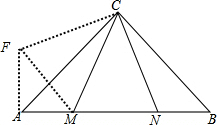
过点A作AF⊥AB,使AF=BN,连接DF,CF,
∵在△ABC中,AC=BC,∠ACB=90°,
∴∠CAB=∠B=45°,
∴∠FAC=45°,
∴△CAF≌△CBN(SAS),
∴CF=CN,
∠ACF=∠BCN,
∵∠ACB=90°,∠DCN=45°,
∴∠ACM+∠BCN=∠ACB-∠MCN=90°-45°=45°,
∵∠ACF=∠BCN,
∴∠ACM+∠ACF=45°,
即∠MCF=45°,
∴∠MCF=∠MCN,
又∵CM=CM,
∴△CMF≌△CMN(SAS),
∴MF=MN,
∵AM2+AF2=MF2,
∴AM2+BM2=MN2;
(2)结论仍然成立;如图,
证明:过点A作AF⊥AB,使AF=BN,连接MF,
∵在△ABC中,AC=BC,∠ACB=90°,
∴∠CAB=∠B=45°,
∴∠FAC=45°,
∴△CAF≌△CBN(SAS),
∴CF=CN,
∠ACF=∠BCN,
∵∠BCN+∠ACN=90°,
∴∠ACF+∠ACN=90°,即∠FCN=90°,
∵∠MCN=45°,
∴∠MCF=45°,
∴∠MCF=∠MCN,
又∵CM=CM,
∴△CMF≌△CMN(SAS),
∴MF=MN,
∵AM2+AF2=MF2,
∴AM2+BN2=MN2.
点评 此题主要考查旋转的性质,勾股定理及三角形全等的判定与性质,解答时要充分分析里面的条件与问题之间的联系.


科目:初中数学 来源: 题型:解答题
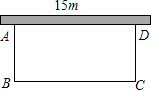 如图,某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成.若设花园的宽为x(m),花园的面积为y (m2).
如图,某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成.若设花园的宽为x(m),花园的面积为y (m2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | $\frac{22}{7}$ | C. | $\sqrt{3}$ | D. | $\sqrt{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com