
【题目】如图,点![]() 分别在
分别在![]() 两边上,且
两边上,且![]() ,以
,以![]() 为直径作半圆
为直径作半圆![]() ,点
,点![]() 是半圆
是半圆![]() 的中点
的中点
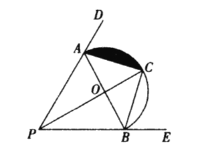
(1)连接![]() ,求证:
,求证: ![]() ;
;
(2)若![]() ,
, ![]() ,求阴影部分面积
,求阴影部分面积
(3)若点![]() 是
是![]() 的外心,判断四边形
的外心,判断四边形![]() 的形状,并说明理由
的形状,并说明理由
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() 是
是![]() 的中点,直线
的中点,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)如图,若点![]() 在线段
在线段![]() 上,线段
上,线段![]() 和
和![]() 之间的数量关系是 ,位置关系是 ;
之间的数量关系是 ,位置关系是 ;
(2)在(1)的条件下,当点![]() 在线段
在线段![]() 上,且
上,且![]() 时,求证:
时,求证:![]() ;
;
(3)当点![]() 在线段
在线段![]() 的延长线上时,在线段
的延长线上时,在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
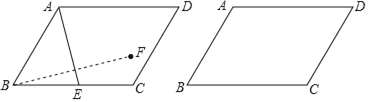
【题目】如图,已知ABCD中,∠ABC=60°,AB=4,BC=m,E为BC边上的动点,连结AE,作点B关于直线AE的对称点F.
(1)若m=6,①当点F恰好落在∠BCD的平分线上时,求BE的长;
②当E、C重合时,求点F到直线BC的距离;
(2)当点F到直线BC的距离d满足条件:2![]() ﹣2≤d≤2
﹣2≤d≤2![]() +4,求m的取值范围.
+4,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地要改造部分农田种植蔬菜.经调查,平均每亩改造费用是![]() 元,添加滴灌设备等费用(元)与改造面积
元,添加滴灌设备等费用(元)与改造面积![]() (亩)的平分成正比,比例系数为
(亩)的平分成正比,比例系数为![]() ,以上两项费用
,以上两项费用![]() 年内不需要增加;每亩种植蔬菜还需种子、人工费用
年内不需要增加;每亩种植蔬菜还需种子、人工费用![]() 元,这项费用每年均需开支.设改造
元,这项费用每年均需开支.设改造![]() 亩,每亩蔬菜年均销售金额为
亩,每亩蔬菜年均销售金额为![]() 元,除上述费用外,没有其他费用.
元,除上述费用外,没有其他费用.
(1)设当年收益为![]() 元,求
元,求![]() 与
与![]() 的函数关系式(用含
的函数关系式(用含![]() 的式子表示);
的式子表示);
(2)若![]() ,如果按
,如果按![]() 年计算,是否改造面积越大收益越大?改造面积为多少时可以得到最大收益?
年计算,是否改造面积越大收益越大?改造面积为多少时可以得到最大收益?
(3)若![]() 时,按
时,按![]() 年计算,能确保改造的面积越大收益也越大,求
年计算,能确保改造的面积越大收益也越大,求![]() 的取值范围.
的取值范围.
注:收益=销售金额-(改造费+滴灌设备等费+种子、人工费)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB=AC.如图,D、E为∠BAC的平分线上的两点,连接BD、CD、BE、CE;如图4, D、E、F为∠BAC的平分线上的三点,连接BD、CD、BE、CE、BF、CF;如图5, D、E、F、G为∠BAC的平分线上的四点,连接BD、CD、BE、CE、BF、CF、BG、CG……依此规律,第17个图形中有全等三角形的对数是( )

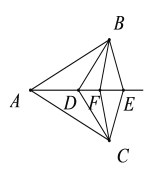

A.17B.54C.153D.171
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题呈现:我们知道反比例函数y=![]() (x>0)的图象是双曲线,那么函数y=
(x>0)的图象是双曲线,那么函数y=![]() +n(k、m、n为常数且k≠0)的图象还是双曲线吗?它与反比例函数y=
+n(k、m、n为常数且k≠0)的图象还是双曲线吗?它与反比例函数y=![]() (x>0)的图象有怎样的关系呢?让我们一起开启探索之旅……
(x>0)的图象有怎样的关系呢?让我们一起开启探索之旅……
探索思考:我们可以借鉴以前研究函数的方法,首先探索函数y=![]() 的图象.
的图象.
(1)填写下表,并画出函数y=![]() 的图象.
的图象.
①列表:
x | … | ﹣5 | ﹣3 | ﹣2 | 0 | 1 | 3 | … |
y | … | … |
②描点并连线.
(2)观察图象,写出该函数图象的两条不同类型的特征:
① ② ;
理解运用:函数y=![]() 的图象是由函数y=
的图象是由函数y=![]() 的图象向 平移 个单位,其对称中心的坐标为 .
的图象向 平移 个单位,其对称中心的坐标为 .
灵活应用:根据上述画函数图象的经验,想一想函数y=![]() +2的图象大致位置,并根据图象指出,当x满足 时,y≥3.
+2的图象大致位置,并根据图象指出,当x满足 时,y≥3.

查看答案和解析>>
科目:初中数学 来源: 题型:
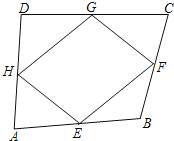
【题目】如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,顺次连接E、F、G、H,若要使四边形EFGH为菱形,则还需增加的条件是( )
A.AC=BDB.AC⊥BDC.AC⊥BD且AC=BDD.AB=AD
查看答案和解析>>
科目:初中数学 来源: 题型:
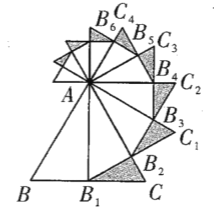
【题目】如图,已知等边![]() 的边长是
的边长是![]() ,以
,以![]() 边上的高
边上的高![]() ,为边作等边三角形,得到第一个等边
,为边作等边三角形,得到第一个等边![]() ;再以等边
;再以等边![]() 的
的![]() 边上的高
边上的高![]() ,为边作等边三角形,得到第二个等边
,为边作等边三角形,得到第二个等边![]() ,再以等边
,再以等边![]() 的
的![]() 边上的高
边上的高![]() 为边作等边三角形,得到第三个等边
为边作等边三角形,得到第三个等边![]() : ....记
: ....记![]() 的面积为
的面积为![]() 的面积为
的面积为![]() 的面积为
的面积为![]() ,如此下去,则
,如此下去,则![]() ___________
___________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com