
【题目】已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
x | … | 1 | 2 | 3 | 5 | 7 | 9 | … |
y | … | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | … |
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整: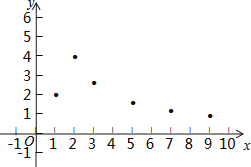
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为
②该函数的一条性质:
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.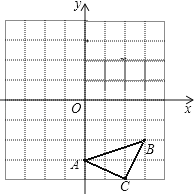
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2 , 使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,△ABC中,AB=AC,点D在BC边上,∠DAB=∠ABD,BE⊥AD,垂足为E,求证:BC=2AE.
小明经探究发现,过点A作AF⊥BC,垂足为F,得到∠AFB=∠BEA,从而可证△ABF≌△BAE(如图2),使问题得到解决.
(1)根据阅读材料回答:△ABF与△BAE全等的条件是 AAS(填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的一个)
参考小明思考问题的方法,解答下列问题:
(2)如图3,△ABC中,AB=AC,∠BAC=90°,D为BC的中点,E为DC的中点,点F在AC的延长线上,且∠CDF=∠EAC,若CF=2,求AB的长;
(3)如图4,△ABC中,AB=AC,∠BAC=120°,点D、E分别在AB、AC边上,且AD=kDB(其中0<k< ![]() ),∠AED=∠BCD,求
),∠AED=∠BCD,求 ![]() 的值(用含k的式子表示).
的值(用含k的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(﹣6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第15次翻转后点C的横坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( ) 
A.不变
B.增大
C.减小
D.先变大再变小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,tan∠C= ![]() ,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )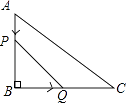
A.18cm2
B.12cm2
C.9cm2
D.3cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AE=CD,AD、BE相交于点P,BQ⊥DA于Q.
(1)求∠BPQ的度数;
(2)若PQ=3,EP=1,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班全体学生2016年初中毕业体育考试的成绩统计如表:
成绩(分) | 35 | 39 | 42 | 44 | 45 | 48 | 50 |
人数(人) | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
根据表中的信息判断,下列结论中错误的是( )
A.该班一共有40名同学
B.该班学生这次考试成绩的众数是45分
C.该班学生这次考试成绩的中位数是45分
D.该班学生这次考试成绩的平均数是45分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com