
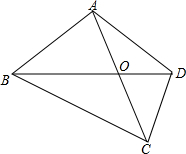
 如图所示,四边形ABCD中,对角线AC、BD交于点O,且AB=AD,AO=OC,请你猜想AB+BO与BC+OD的数量关系,并证明你的结论.
如图所示,四边形ABCD中,对角线AC、BD交于点O,且AB=AD,AO=OC,请你猜想AB+BO与BC+OD的数量关系,并证明你的结论. 分析 分三种情况:若OB>DO,在BO上取点E使OE=OD,连接AE,CE,则四边形AECD是平行四边形,根据平行四边形的性质得到AD=CE,于是得到BC-AB=BC-AD=BC-CE<BE=OB-OE=OB-OD,即可求得AB+BO>BC+DO;②若OB<DO,同理得到AB+BO∠BC+OD,若OB=OD,同理得到AB+OB=BC+OD.
解答 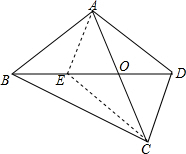 解:①若OB>DO,在BO上取点E使OE=OD,连接AE,CE,则四边形AECD是平行四边形,
解:①若OB>DO,在BO上取点E使OE=OD,连接AE,CE,则四边形AECD是平行四边形,
∴AD=CE,
∴BC-AB=BC-AD=BC-CE<BE=OB-OE=OB-OD,
∴AB+BO>BC+DO;
②若OB<DO,同理得到AB+BO∠BC+OD,
③若OB=OD,同理得到AB+OB=BC+OD.
点评 本题考查了平行四边形的判定和性质,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图所示,在△ABC中,AB=AC,BD=CD,DE⊥AB于E,DF⊥AC于F,G为边BC上与点B,D,C不重合的任意一点,GH⊥AB于H,GM⊥AC于M;求证:GH+GM=DE+DF.
如图所示,在△ABC中,AB=AC,BD=CD,DE⊥AB于E,DF⊥AC于F,G为边BC上与点B,D,C不重合的任意一点,GH⊥AB于H,GM⊥AC于M;求证:GH+GM=DE+DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知正方形ABCD的边长为3cm,以CD为边向CD的两旁分别作等边△PCD和等边△QCD.
如图,已知正方形ABCD的边长为3cm,以CD为边向CD的两旁分别作等边△PCD和等边△QCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com