
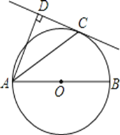
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.
(1)求证:DC为⊙O的切线;
(2)若∠DAB=60°,⊙O的半径为3,求线段AC的长.
【答案】(1)见解析;(2) ![]() .
.
【解析】
(1)连结OC,如图,根据角平分线定义得∴∠DAC=∠OAC,加上∠OAC=∠OCA,则∠DAC=∠OCA,于是可判断OC∥AD,由于AD⊥DC,所以OC⊥DC,则可根据切线的判定定理得到结论;
(2)连结BC,如图,在Rt△ABC中,根据勾股定理可求得答案.
(1)证明: 连接OC
∵ OA=OC
∴ ∠OAC=∠OCA
∵ AC平分∠DAB
∴ ∠DAC=∠OAC
∴ ∠DAC=∠OCA
∴ OC∥AD
∴ ∠ADC+∠OCD=180°
∵ AD⊥CD
∴ ∠ADC =90°
∴ ∠OCD=90°
∴ OC⊥CD
又∵OC是⊙O的半径
∴ 直线CD是⊙O的切线;
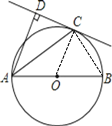
(2)连接BC
∵ AB为⊙O的直径,
∴ ∠ACB=90°.
∵ AC平分∠DAB , ∠DAB=60°,
∴ ∠CAB=30°.
∵ ⊙O的半径为3,
∴ AB=6.
∴ BC=3.
在Rt△ABC中,根据勾股定理,得 AC2+BC2 =AB2
∴ AC2+32 = 62.
∴ AC=![]() .
.


科目:初中数学 来源: 题型:
【题目】某商场举办抽奖活动,规则如下:在不透明的袋子中有2个红球和2个黑球,这些球除颜色外都相同,顾客每次摸出一个球,若摸到红球,则获得1份奖品,若摸到黑球,则没有奖品。
(1)如果小芳只有一次摸球机会,那么小芳获得奖品的概率为 ;
(2)如果小芳有两次摸球机会(摸出后不放回),求小芳获得2份奖品的概率。(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,学校准备在如图所示的矩形ABCD空地上进行绿化,规划在中间的一块四边形MNPQ上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ,已知BC=30米,AB=42米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.
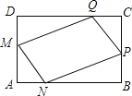
(1)分别求y1和y2与x之间的函数关系式(不要求写出自变量的取值范围);
(2)当AN的长为多少米时,种花的面积为640平方米?
(3)若种花每平方米需200元,铺设草坪每平方米需100元,现设计要求种花的面积不大于640平方米,设学校所需费用W(元),求W与x之间的函数关系式,并求出学校所需费用的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.
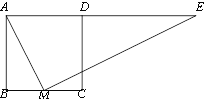
(1)求证:△ABM ∽△EMA;
(2)若AB=2,BM=1,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.
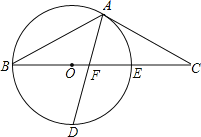
(1)求证:AC是⊙O的切线:
(2)若BF=8,DF=![]() ,求⊙O的半径r.
,求⊙O的半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝新中国成立70周年,河南省实验中学开展了以“我和我亲爱的祖国”为主题的“快闪”活动,九年级准备从两名男生和两名女生中选出两名同学领唱,如果每一位同学被选中的机会均等,则选出的恰为一位男生一位女生的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
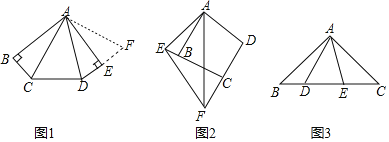
【题目】(1)操作发现
如图1,在五边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,试猜想
,试猜想![]() ,
,![]() ,
,![]() 之间的数量关.小明地过仔细思考,得到如下解题思路:
之间的数量关.小明地过仔细思考,得到如下解题思路:
将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() .由
.由![]() ,得
,得![]() ,即点
,即点![]() ,
,![]() ,
,![]() 三点共线,易证
三点共线,易证![]() _____,被
_____,被![]() ,
,![]() ,
,![]() 之间的数量关系是_______;
之间的数量关系是_______;
(2)类比探究
如图2,在四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 的延长线上,
的延长线上,![]() ,连接
,连接![]() ,试猜想
,试猜想![]() ,
,![]() ,
,![]() 之间的数量关系,并给出证明.
之间的数量关系,并给出证明.
(3)拓展延伸
如图3,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 均在边
均在边![]() 上,且
上,且![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为_____.
的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AC于点E,交BC于点F,连接BE、DF,且BE平分∠ABD.
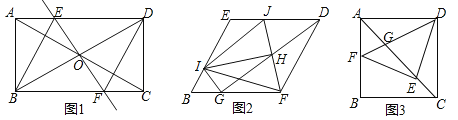
(1)①求证:四边形BFDE是菱形;②求∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的数量关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一跨河桥,桥拱是圆弧形,跨度(AB)为16米,拱高(CD)为4米,求:
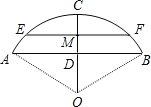
(1)桥拱半径.
(2)若大雨过后,桥下河面宽度(EF)为12米,求水面涨高了多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com