
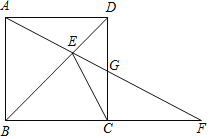
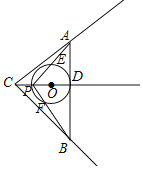
【题目】如图,在正方形ABCD中,点E是对角线BD上任意一点,连接AE并延长AE交BC的延长线于点F,交CD于点G.
(1)求证:∠DAE=∠DCE;
(2)若∠F=30°,DG=2,求CG的长度.
【答案】(1)见解析;(2)CG=2![]() ﹣2
﹣2
【解析】
(1)根据正方形的性质得出∠ADE=∠CDE,AD=CD,根据全等三角形的判定推出△ADE≌△CDE,则结论可得;
(2)根据正方形的性质得出AD=DC,∠ADC=90°,AD∥BC,求出∠F=∠DAG=30°,解直角三角形求出AD,即可得出答案.
(1)证明:∵四边形ABCD是正方形,
∴∠ADE=∠CDE,AD=CD,
在△ADE和△CDE中
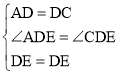
∴△ADE≌△CDE(SAS),
∴∠DAE=∠DCE;
(2)解:∵四边形ABCD是正方形,
∴AD=DC,∠ADC=90°,AD∥BC,
∴∠DAG=∠F,
∵∠F=30°,
∴∠DAG=30°,
∵DG=2,
∴AG=2DG=4,
由勾股定理得:AD=![]() =
=![]() =2
=2![]() ,
,
∴DC=AD=2![]() ,
,
∴CG=CD﹣DG=2![]() ﹣2.
﹣2.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
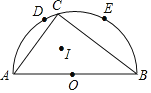
【题目】如图,已知点D,E是半圆O上的三等分点,C是弧DE上的一个动点,连结AC和BC,点I是△ABC的内心,若⊙O的半径为3,当点C从点D运动到点E时,点I随之运动形成的路径长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解本校学生平均每天的体育活动时间情况,随机抽取部分学生进行问卷调查,并将调查结果人数分为A,B,C,D四个等级设活动时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.
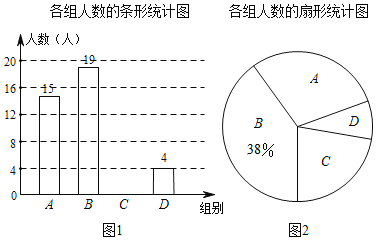
请你根据图中信息解答下列问题:
(1)该校共调查了多少名学生;
(2)将条形统计图补充完整;
(3)求出表示A等级的扇形圆心角的度数;
(4)在此次问卷调查中,甲班有2人平均每天大课间活动时间不足1小时,乙班有3人平均每天大课间活动时间不足1小时,若从这5人中任选2人去参加座谈,试用列表或画树状图的方法求选出的2人来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=7,BC=4![]() ,∠ABC=45°,射线CD⊥AB于D,点P为射线CD上一动点,以PD为直径的⊙O交PA、PB分别为E、F,设CP=x.
,∠ABC=45°,射线CD⊥AB于D,点P为射线CD上一动点,以PD为直径的⊙O交PA、PB分别为E、F,设CP=x.
(1)求sin∠ACD的值.
(2)在点P的整个运动过程中:
①当⊙O与射线CA相切时,求出所有满足条件时x的值;
②当x为何值时,四边形DEPF为矩形,并求出矩形DEPF的面积.
(3)如果将△ADC绕点D顺时针旋转150°,得△A′DC′,若点A′和点C′有且只有一个点在圆内,则x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:规定max(a,b)=![]() ,例如:max(﹣1,2)=2,max(3,3)=3.
,例如:max(﹣1,2)=2,max(3,3)=3.
感知:已知函数y=max(x+1,﹣2x+4)
(1)当x=3时,y=_____;
(2)当y=3时,x=______;
(3)当y随x的增大而增大时,x的取值范围为______;
(4)当﹣1≤x≤4时,y的取值范围为______;
探究:已知函数y=max(x+2,![]() )当直线y=m(m为常数)与函数y=max(x+2,
)当直线y=m(m为常数)与函数y=max(x+2,![]() )(﹣6<x≤3)的图象有两个公共点时,m的取值范围为_______;
)(﹣6<x≤3)的图象有两个公共点时,m的取值范围为_______;
拓展:已知函数y=max(﹣x2+2nx,﹣nx)(n为常数且n≠0),当![]() n﹣3≤x≤2时,随着x的增大,函数值y先减小后增大,直接写出n的取值范围.
n﹣3≤x≤2时,随着x的增大,函数值y先减小后增大,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着私家车的增多,“停车难”成了很多小区的棘手问题.某小区为解决这个问题,拟建造一个地下停车库.如图是该地下停车库坡道入口的设计示意图,其中,入口处斜坡![]() 的坡角为
的坡角为![]() ,水平线
,水平线![]() .根据规定,地下停车库坡道入口上方要张贴限高标志,以提醒驾驶员所驾车辆能否安全驶入.请求出限制高度为多少米,(结果精确到
.根据规定,地下停车库坡道入口上方要张贴限高标志,以提醒驾驶员所驾车辆能否安全驶入.请求出限制高度为多少米,(结果精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市民广场有一个直径16米的圆形喷水池,喷水池的周边有一圈喷水头(喷水头高度忽略不计),各方向喷出的水柱恰好在喷水池中心的装饰物OA的顶端A处汇合,水柱离中心3米处达最高5米,如图所示建立直角坐标系.王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的他站立时必须在离水池中心O________米以内.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com