(1)求∠BOE的度数；

(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围；若不变，求出这个比值（提示:图中∠OFC=∠BOF+∠OBC）；

(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出∠OEC度数；若不存在,说明理由(提示：三角形三个内角的和为180）.

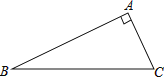
（1）按要求作图：（保留作图痕迹）

①延长BC到点D，使CD=BC；

②延长CA到点E，使AE=2CA；

③连接AD，BE并猜想线段 AD与BE的大小关系；

（2）证明（1）中你对线段AD与BE大小关系的猜想．

①a∥b；②b∥c；③a∥c；④a⊥b；⑤a⊥c．

以其中两个论断作为题设，一个论断作为结论，组成一个你认为不正确的命题是(　　)

A.已知①②则③B.已知②⑤则④C.已知②④则③D.已知④⑤则②

A.(4，3)B.(4，2)C.(2，3)D.(3，2)

【题目】数学老师在课堂上提出一个问题：“通过探究知道： ≈1.414…，它是个无限不循环小数，也叫无理数，它的整数部分是1，那么有谁能说出它的小数部分是多少”，小明举手回答：它的小数部分我们无法全部写出来，但可以用﹣1来表示它的小数部分，张老师夸奖小明真聪明，肯定了他的说法．现请你根据小明的说法解答：

（1）的小数部分是a， 的整数部分是b，求a+b﹣的值．

（2）已知8+=x+y，其中x是一个整数，0＜y＜1，求3x+（y﹣）2018的值．

①

②

③

④

其中成立的有（　　）

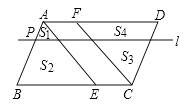
A. ①②④ B. ②③ C. ②③④ D. ③④

已知，如图所示，BCE，AFE是直线，

AB∥CD，∠1=∠2，∠3=∠4．

求证：AD∥BE

证明：∵ AB∥CD （已知）

∴ ∠4 =∠ （ ）

∵ ∠3 =∠4 （已知）

∴ ∠3 =∠ （ ）

∵ ∠1 =∠2 （已知）

∴ ∠1+∠CAF =∠2+ ∠CAF ( )

即：∠ =∠ ．

∴ ∠3 =∠ （ ）

∴ AD∥BE （ ）

第一个等式：

第二个等式：

第三个等式：

第四个等式：

则式子__________________；

用含n的代数式表示第n个等式： ____________________________；