
科目: 来源: 题型:
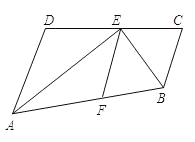
【题目】如图,点E在线段CD上,EA、EB分别平分∠DAB和∠CBA,点F在线段AB上运动,AD=4cm,BC=3cm,且AD∥BC.
(1)你认为AE和BE有什么位置关系?并验证你的结论;
(2)当点F运动到离点A多少厘米时,△ADE和△AFE全等?为什么?
(3)在(2)的情况下,此时BF=BC吗?证明你的结论并求出AB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,池塘边有块长为20m,宽为10m的长方形土地,现在将其余三面留出宽都是xm的小路,中间余下的长方形部分做菜地,用含x的式子表示:
(1)菜地的长a= m,菜地的宽b= m;菜地的周长C= m;
(2)求当x=1m时,菜地的周长C.

查看答案和解析>>
科目: 来源: 题型:
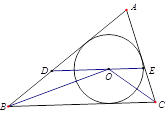
【题目】如图,⊙O是△ABC的内切圆,过点O作DE∥BC,与AB、AC分别交于点D、E.
(1)求证:BD+CE=DE;
(2)若∠BAC=70,求∠BOC的度数
查看答案和解析>>
科目: 来源: 题型:
【题目】某钢铁企业为了适应市场竞争的需要,提高生产效率,决定将一部分钢铁生产一线员工调整去从事服务工作,该企业有钢铁生产一线员工1000人,平均每人可创造年产值30万元,根据规划,调整出去的一部分一线员工后,余下的生产一线员工平均每人全年创造年产值可增加30%,调整到服务性工作岗位人员平均每人全年可创造产值24万元,如果要保证员工岗位调整后,现在全年总产值至少增加20%,且钢铁产品的产值不能超过33150万元,怎样安排调整到服务行业的人数?
查看答案和解析>>
科目: 来源: 题型:
【题目】根据下表中的二次函数y=ax2+bx+c的自变量x与函数y的对应值,可判断二次函数的解析式为( )
x | … |
| 0 | 1 | 2 | … |
y | … |
|
|
|
| … |
A. y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() B. y=
B. y=![]() x2+
x2+![]() x﹣
x﹣![]()
C. y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() D. y=﹣
D. y=﹣![]() x2+
x2+![]() x+
x+![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外都相同,其中红球有1个,若从中随机摸出一个球,这个球是白球的概率为![]() .
.
(1)求袋子中白球的个数;(请通过列式或列方程解答)
(2)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
查看答案和解析>>
科目: 来源: 题型:
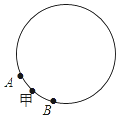
【题目】如图,A和B两个小机器人,自甲处同时出发相背而行,绕直径为整数米的圆周上运动,15分钟内相遇7次,如果A的速度每分钟增加6米,则A和B在15分钟内相遇9次,问圆周直径至多是多少米?至少是多少米?(取π=3.14)
查看答案和解析>>
科目: 来源: 题型:
【题目】若如图,已知AD∥BC,按要求完成下列各小题(保留作图痕迹,不要求写作法).
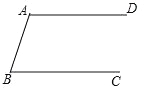
(1)用直尺和圆规作出∠BAD的平分线AP,交BC于点P.
(2)在(1)的基础上,若∠APB=55°,求∠B的度数.
(3)在(1)的基础上,E是AP的中点,连接BE并延长,交AD于点F,连接PF.求证:四边形ABPF是菱形.
查看答案和解析>>
科目: 来源: 题型:
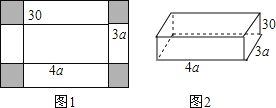
【题目】一张如图1的长方形铁皮,四个角都剪去边长为30厘米的正方形,再四周折起,做成一个有底无盖的铁盒如图2,铁盒底面长方形的长是4a(cm),宽是3a(cm),这个无盖铁盒各个面的面积之和称为铁盒的全面积.
(1)请用a的代数式表示图1中原长方形铁皮的面积;
(2)若要在铁盒的各个外表面漆上某种油漆,每元钱可漆的面积为![]() (cm2),则油漆这个铁盒需要多少钱(用a的代数式表示)?
(cm2),则油漆这个铁盒需要多少钱(用a的代数式表示)?
(3)铁盒的底面积是全面积的几分之几(用a的代数式表示)?若铁盒的底面积是全面积的![]() ,求a的值;
,求a的值;
(4)是否存在一个正整数a,使得铁盒的全面积是底面积的正整数倍?若存在,请求出这个a,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com