（1）本次调查共抽取了多少名学生？

（2）求在被调查的学生中，最喜爱教师职业的人数，并补全条形统计图；

（3）若海静中学共有1500名学生，请你估计该中学最喜爱律师职业的学生有多少名？

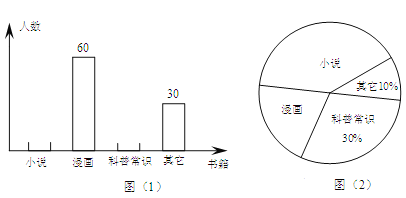
A. 由这两个统计图可知喜欢“科普常识”的学生有90人．

B. 若该年级共有1200名学生，则由这两个统计图可估计喜爱“科普常识”的学生约有360个．

C. 由这两个统计图不能确定喜欢“小说”的人数．

D. 在扇形统计图中，“漫画”所在扇形的圆心角为72°．

A. 扇形甲的圆心角是72° B. 学生的总人数是90人

C. 初三的人数比初二的人数多10人 D. 初一的人数比初三的人数少15人

【题目】如图，AB∥CD，直线EF与AB，CD分别交于点M，N，过点N的直线GH与AB交于点P，则下列结论错误的是（　　）

A.∠EMB=∠END
B.∠BMN=∠MNC
C.∠CNH=∠BPG
D.∠DNG=∠AME

【题目】端午节前夕，小东的父母准备购买若干个粽子和咸鸭蛋(每个粽子的价格相同，每个咸鸭蛋的价格相同)．已知粽子的价格比咸鸭蛋的价格贵1.5元，花35元购买粽子的个数与花20元购买咸鸭蛋的个数相同．粽子与咸鸭蛋的价格各是多少？

【答案】粽子和咸鸭蛋的单价分别为每个3.5元、2元

【解析】试题分析：设咸鸭蛋的价格为x元，则粽子的价格为（1.5＋x）元，根据花35元购买粽子的个数与花20元购买咸鸭蛋的个数相同，列出分式方程，求出方程的解得到x的值，即可得到结果．

试题解析：

解：设咸鸭蛋的价格为x元，则粽子的价格为（1.5＋x）元，

根据题意得：

，

去分母得：35x＝30＋20x，

解得：x＝2，

经检验x＝2是分式方程的解，且符合题意，

1.5＋x＝1.5＋2＝3.5（元），

故咸鸭蛋的价格为2元，粽子的价格为3.5元．

点睛：此题考查了分式方程的应用，分析题意，找到合适的等量关系是解决问题的关键．

【题型】解答题
【结束】
24

【题目】某校为了开展读书月活动，对学生最喜欢的图书种类进行了一次抽样调查，所有图书分成四类：艺术、文学、科普、其他．随机调查了该校m名学生(每名学生必选且只能选择一类图书)，并将调查结果制成如下两幅不完整的统计图：

根据统计图提供的信息，解答下列问题：

(1)m＝ ，n＝ ；

(2)扇形统计图中，“艺术”所对应的扇形的圆心角度数是 度；

(3)请根据以上信息补全条形统计图；

(4)根据抽样调查的结果，请你估计该校1000名学生中有多少学生最喜欢科普类图书．

【答案】 (1)m=50， n=30；（2）72度 (3)补图见解析（4）300

【解析】试题分析：（1）根据其他的人数和所占的百分比即可求得m的值，从而可以求得n的值；

（2）根据扇形统计图中的数据可以求得“艺术”所对应的扇形的圆心角度数；

（3）根据题意可以求得喜爱文学的人数，从而可以将条形统计图补充完整；

（4）根据统计图中的数据可以估计该校600名学生中有多少学生最喜欢科普类图书．

试题解析：

解：（1）m＝5÷10%＝50，n%＝15÷50＝30%，

故答案为：50，30；

（2）由题意可得，

“艺术”所对应的扇形的圆心角度数是：360°×＝72°，

故答案为：72；

（3）文学有：50－10－15－5＝20，

补全的条形统计图如图所示；

（4）由题意可得，

600×＝180，

即该校600名学生中有180名学生最喜欢科普类图书．

点睛：本题考查条形统计图、扇形统计图、用样本估计总体，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．

【题型】解答题
【结束】
23

【题目】已知，m，n是一元二次方程x2+4x+3=0的两个实数根，且|m|＜|n|，抛物线y=x2+bx+c的图象经过点A（m，0），B（0，n），如图所示．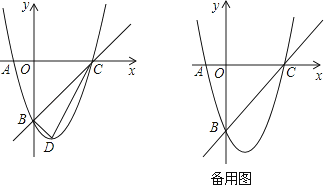
（1）求这个抛物线的解析式；
（2）设（1）中的抛物线与x轴的另一个交点为抛物线的顶点为D，试求出点C，D的坐标，并判断△BCD的形状；
（3）点P是直线BC上的一个动点（点P不与点B和点C重合），过点P作x轴的垂线，交抛物线于点M，点Q在直线BC上，距离点P为 个单位长度，设点P的横坐标为t，△PMQ的面积为S，求出S与t之间的函数关系式．

A. 4月份商场的商品销售总额是75万元 B. 1月份商场服装部的销售额是22万元

C. 5月份商场服装部的销售额比4月份减少了 D. 3月份商场服装部的销售额比2月份减少了

【题目】解分式方程：

(1) (2)

【答案】(1) ;(2)x=

【解析】试题分析：（1）两边乘以(x－1)(2x＋1)去分母，转化为整式方程，然后解整式方程，检验后写出分式方程的解即可；

（2）两边乘以(x＋2)(x－2)去分母，转化为整式方程，然后解整式方程，检验后写出分式方程的解即可．

试题解析：

解：（1）两边乘以(x－1)(2x＋1)去分母得：2x＋1＝5(x－1)，

解得：x＝2，

当x＝2时，(x－1)(2x＋1)≠0，

∴原分式方程的解为x＝2；

（2）两边乘以(x＋2)(x－2)去分母得：(x－2)2－3＝(x＋2)(x－2)，

解得：x＝，

当x＝时，(x＋2)(x－2)≠0，

所以原分式方程的解为x＝．

【题型】解答题
【结束】
21

【题目】先化简，再求值，其中的值从不等式组的整数解中选取.

【题目】计算:

（1） (2)

(3) (4)

【答案】(1) ;(2) ;(3) ; (4)

【解析】试题分析：（1）分子、分母分解因式后约分即可；

（2）先通分计算括号内分式的减法，然后把除法转化为乘法，分子、分母分解因式后约分即可；

（3）第二个分式分子、分母分解因式后约分，然后通分转化为同分母分式，最后依照同分母分式的加减法则计算即可；

（4）先通分计算括号内分式的减法，然后把除法转化为乘法，分子、分母分解因式后约分即可．

试题解析：

解：（1）原式＝

＝；

（2）原式＝

＝

＝；

（3）原式＝

＝

＝

＝

＝；

（4）原式＝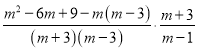

＝

＝．

点睛：此题考查了分式的混合运算，熟练掌握运算法则和运算顺序是解本题的关键．

【题型】解答题
【结束】
20

(1) (2)