
科目: 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作Rt△ABC,使其斜边AB=c,一条直角边BC=a.
已知线段a,c如图.
小芸的作法如下:
①取AB=c,作AB的垂直平分线交AB于点O;
②以点O为圆心,OB长为半径画圆;
③以点B为圆心,a长为半径画弧,与⊙O交于点C;
④连接BC,AC.
则Rt△ABC即为所求.
老师说:“小芸的作法正确.”
请回答:小芸的作法中判断∠ACB是直角的依据是 
查看答案和解析>>
科目: 来源: 题型:
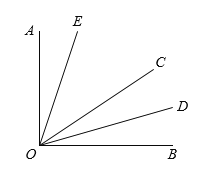
【题目】如图,∠AOC与∠BOC互余,OD平分∠BOC,∠EOC=2∠AOE.
(1)若∠AOD=75°,求∠AOE的度数.
(2)若∠DOE=54°,求∠EOC的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】老师在课堂上出了一个问题:若点A(﹣2,y1),B(1,y2)和C(4,y3)都在反比例函数y=![]() 的图象上,比较y1 , y2 , y3的大小.
的图象上,比较y1 , y2 , y3的大小.
小明是这样思考的:当k<0时,反比例函数的图象是y随x的增大而增大的,并且﹣2<1<4,所以y1<y2<y3 .
你认为小明的思考 (填“正确”和“不正确”),理由是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】已知C为线段AB的中点,E为线段AB上的点,点D为线段AE的中点.
(1)若线段AB=a,CE=b,|a﹣15|+(b﹣4.5)2=0,求a,b的值;
(2)如图1,在(1)的条件下,求线段DE的长;
(3)如图2,若AB=15,AD=2BE,求线段CE的长.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九勾股,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”
译文:“今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)
你的计算结果是:出南门 步而见木.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地下车库出口处安装了“两段式栏杆”,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图所示的位置,其中AB⊥BC,EF∥BC,∠AEF=135°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为(栏杆宽度忽略不计.参考数据:![]() ≈1.4)( )
≈1.4)( )
A.
B.
C.
D.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在平行四边形ABCD中,连接BD,AD=6cm,BD=8cm,∠DBC=90°,现将△AEF沿BD的方向匀速平移,速度为2cm/s,同时,点G从点D出发,沿DC的方向匀速移动,速度为2cm/s.当△AEF停止移动时,点G也停止运动,连接AD,AG,EG,过点E作EH⊥CD于点H,如图2所示,设△AEF的移动时间为t(s)(0<t<4).
(1)当t=1时,求EH的长度;
(2)若EG⊥AG,求证:EG2=AEHG;
(3)设△AGD的面积为y(cm2),当t为何值时,y可取得最大值,并求y的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,点C在线段AB上,AC = 8 cm,CB = 6 cm,点M、N分别是AC、BC的中点.
![]()
(1)求线段MN的长.
(2)若C为线段AB上任意一点,满足AC+CB=a(cm),其他条件不变,你能猜想出MN的长度吗?并说明理由.
(3)若C在线段AB的延长线上,且满足AC-CB=b(cm),M、N分别为AC、BC的中点,你能猜想出MN的长度吗?请画出图形,写出你的结论,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离,即|x|=|x﹣0|,也就是说|x|表示在数轴上数x与数0对应点之间的距离;这个结论可以推广为:|x﹣y|表示在数轴上数x、y对应点之间的距离;在解题中,我们常常运用绝对值的几何意义.
①解方程|x|=2,容易看出,在数轴上与原点距离为2的点对应的数为±2,即该方程的解为x=±2.
②在方程|x﹣1|=2中,x的值就是数轴上到1的距离为2的点对应的数,显然x=3或x=﹣1.
③在方程|x﹣1|+|x+2|=5中,显然该方程表示数轴上与1和﹣2的距离之和为5 的点对应的x值,在数轴上1和﹣2的距离为3,满足方程的x的对应点在1的右边或﹣2的左边.若x的对应点在1的右边,由图示可知,x=2;同理,若x的对应点在﹣2的左边,可得x=﹣3,所以原方程的解是x=2或x=﹣3.根据上面的阅读材料,解答下列问题:
(1)方程|x|=5的解是_______________.
(2)方程|x﹣2|=3的解是_________________.
(3)画出图示,解方程|x﹣3|+|x+2|=9.

查看答案和解析>>
科目: 来源: 题型:
【题目】小明是个爱探究的学生,在学习完等腰三角形的判定定理之后,对于等腰![]() (如图甲),若
(如图甲),若![]() ,
,![]() ,小明发现,只要作
,小明发现,只要作![]() 的平分线就可以将
的平分线就可以将![]() 分成两个等腰三角形.
分成两个等腰三角形.
(1)你认为小明的发现正确吗?若正确,请给出证明过程;若不正确,请说明理由;
(2)请你对图乙的三角形进行探索,将![]() 分成两个等腰三角形,并写出顶角度数;
分成两个等腰三角形,并写出顶角度数;
(3)请你对图丙的三角形进行再探索,将![]() 分成三个等腰三角形,并写出顶角度数.
分成三个等腰三角形,并写出顶角度数.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com