
科目: 来源: 题型:
【题目】已知分式A=![]() .
.
(1) 化简这个分式;
(2) 当a>2时,把分式A化简结果的分子与分母同时加上3后得到分式B,问:分式B的值较原来分式A的值是变大了还是变小了?试说明理由.
(3) 若A的值是整数,且a也为整数,求出符合条件的所有a值的和.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,正方形ABCO的对角线BO在x 轴上,若正方形ABCO的边长为
中,正方形ABCO的对角线BO在x 轴上,若正方形ABCO的边长为![]() ,点B在x负半轴上,反比例函数
,点B在x负半轴上,反比例函数![]() 的图象经过C点.
的图象经过C点.
(1)求该反比例函数的解析式;
(2)当函数值![]() >-2时,请直接写出自变量x的取值范围;
>-2时,请直接写出自变量x的取值范围;
(3)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】在有理数的原有运算法则中,我们补充定义一种新运算“★”如下:a★b=(a+b)(a﹣b),例如:5★3=(5+3)×(5﹣3)=8×2=16,下面给出了关于这种新运算的几个结论:① 3★(﹣2)=5;②a★b=b★a;③若b=0,则a★b=a2;④若a★b=0,则a=b.其中正确结论的有__;(只填序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学组织学生到离学校15千米的兴化生态园进行春季社会实践活动,先遣队与大队同时出发,先遣队的速度是大队速度的1.2倍,结果先遣队比大队早到30分钟,求先遣队的速度和大队速度.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:在△PAB的边PA、PB上分别取点C、D,连接CD使CD∥AB.将△PCD绕点P按逆时针方向旋转得到△PC′D′(∠APC′<∠APB),连接AC′、BD′.
(1)如图1, 若∠APB=90°,PA=PB,求证:AC′=BD′;AC′⊥BD′.
(2)在图1中,连接AD′、BC′,分别取AB、AD′、C′D′、BC′的中点E、F、G、H,顺次连接E、F、G、H得到四边形EFGH.请判断四边形EFGH的形状,并说明理由.
(3)①如图2, 若改变(1)中∠APB的大小,使0°<∠APB<90°,其他条件不变,重复(2)中操作.请你直接判断四边形EFGH的形状.
②如图3,若改变(1)中PA、PB的大小关系,使PA<PB,其他条件不变,重复(2)中操作,请你直接判断是四边形EFGH的形状.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形![]() 的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数
的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数![]() 的图象上,点D的坐标为
的图象上,点D的坐标为![]() .将菱形ABCD沿x轴正方向平移____个单位,可以使菱形的另一个顶点恰好落在该函数图象上.
.将菱形ABCD沿x轴正方向平移____个单位,可以使菱形的另一个顶点恰好落在该函数图象上.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时.求证:CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;
①请直接写出CF,BC,CD三条线段之间的关系;
②若正方形ADEF的边长为2![]() ,对角线AE,DF相交于点O,连接OC.求OC的长度.
,对角线AE,DF相交于点O,连接OC.求OC的长度.

查看答案和解析>>
科目: 来源: 题型:
【题目】某商场将进价为4000元的电视以4400元售出,平均每天能售出6台.为了配合国家财政推出的“节能家电补贴政策”的实施,商场决定采取适当的降价措施,调查发现:这种电视的售价每降价50元,平均每天就能多售出3台.
(1)现设每台电视降价x元,商场每天销售这种电视的利润是y元,请写出y与x之间的函数表达式.(不要求写出自变量的取值范围)
(2)每台电视降价多少元时,商场每天销售这种电视的利润最高?最高利润是多少?
(3)商场要想在这种电视销售中每天盈利3600元,同时又要使百姓得到更多实惠,每台电视应降价多少元?根据以上的结论,请你直接写出售价在什么范围时,每个月的利润不低于3600元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某班研究性学习小组在一次综合实践活动中发现如下问题:在楼底的B处测得河对岸大厦上悬挂的条幅底端D的仰角为26°,在楼顶A处测得条幅顶端C的仰角为50°.若楼AB高度为18米,条幅CD长度为46米,请你帮助他们求出楼与大厦之间的距离BE及大厦的高度CE.(参考数据:sin26°≈0.44,sin50°≈0.77,tan26°≈0.49,tan50°≈1.19).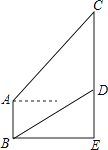
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com