
科目: 来源: 题型:
【题目】如图,已知直线l∥AB,l与AB之间的距离为2.C、D是直线l上两个动点(点C在D点的左侧),且AB=CD=5.连接AC、BC、BD,将△ABC沿BC折叠得到△A′BC.下列说法:①四边形ABCD的面积始终为10;②当A′与D重合时,四边形ABDC是菱形;③当A′与D不重合时,连接A′、D,则∠CA′D+∠BCA′=180°;④若以A′、C、B、D为顶点的四边形为矩形,则此矩形相邻两边之和为3![]() 或7.其中正确的是( )
或7.其中正确的是( )

A. ①②④ B. ①③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平行四边形ABCD的面积是16,对角线AC、BD相交于点O,点M1、N1、P1分别为线段OD、DC、CO的中点,顺次连接M1N1、N1 P1、P1M1得到第一个△P1M1N1 , 面积为S1 , 分别取M1N1、N1P1、P1M1三边的中点P2、M2、N2 , 得到第二个△P2M2N2 , 面积记为S2 , 如此继续下去得到第n个△PnMnNn , 面积记为Sn , 则Sn﹣Sn﹣1= . (用含n的代数式表示,n≥2,n为整数)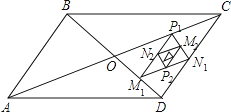
查看答案和解析>>
科目: 来源: 题型:
【题目】有若干个数,第一个数记为a1,第二个数记为a2,第三个数记为a3,…,第n个数记为an,若a1=![]() ,从第二个数起,每个数都等于“1与它前面那个数差的倒数”.
,从第二个数起,每个数都等于“1与它前面那个数差的倒数”.
(1)计算:a2 ,a3 ,a4 ,a5的值;
(2)这排数有什么规律?由你发现的规律,计算a2014的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,小浩从二次函数y=ax2+bx+c(a≠0)的图象中得到如下信息:
①ab<0
②4a+b=0
③当y=5时只能得x=0
④关于x的一元二次方程ax2+bx+c=10有两个不相等的实数根,
你认为其中正确的有( )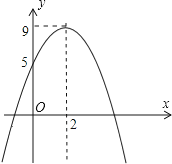
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读理解:
把两个相同的数连接在一起就得到一个新数,我们把它称为“连接数”,例如:234234,3939…等,都是连接数,其中,234234称为六位连接数,3939称为四位连接数.
(1)请写出一个六位连接数 ,它 (填“能”或“不能”)被13整除.
(2)是否任意六位连接数,都能被13整除,请说明理由.
(3)若一个四位连接数记为M,它的各位数字之和的3倍记为N,M﹣N的结果能被13整除,这样的四位连接数有几个?
查看答案和解析>>
科目: 来源: 题型:
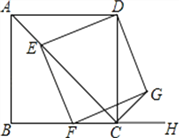
【题目】如图,已知四边形ABCD为正方形,AB=![]() ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的关系解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由; 
(3)在平面直角坐标系中,是否存在点Q,使△BCQ是以BC为腰的等腰直角三角形?若存在,直接写出点Q的坐标;若不存在,说明理由;
(4)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于x轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
(5)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某农产品生产基地收获红薯192吨,准备运给甲、乙两地的承包商进行包销.该基地用大、小两种货车共18辆恰好能一次性运完这批红薯,已知这两种货车的载重量分别为14吨/吨和8吨/辆,运往甲、乙两地的运费如下表:
车型 | 运费 | |
运往甲地/(元/辆) | 运往乙地/(元/辆) | |
大货车 | 720 | 800 |
小货车 | 500 | 650 |
(1)求这两种货车各用多少辆;
(2)如果安排10辆货车前往甲地,其余货车前往乙地,其中前往甲地的大货车为a辆,总运费为w元,求w关于a的函数关系式;
(2)在(2)的条件下,若甲地的承包商包销的红薯不少于96吨,请你设计出使总运费最低的货车调配方案,并求出最低总运费.
查看答案和解析>>
科目: 来源: 题型:
【题目】根据要求回答问题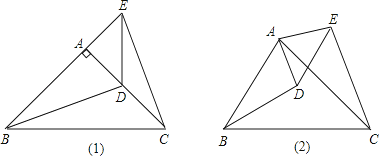
(1)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
①当点D在AC上时,如图1,线段BD、CE有怎样的数量关系和位置关系?直接写出你猜想的结论;
②将图1中的△ADE绕点A顺时针旋转α角(0°<α<90°),如图2,线段BD、CE有怎样的数量关系和位置关系?请说明理由.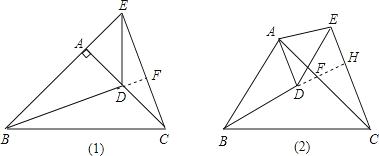
(2)当△ABC和△ADE满足下面甲、乙、丙中的哪个条件时,使线段BD、CE在(1)中的位置关系仍然成立?不必说明理由.
甲:AB:AC=AD:AE=1,∠BAC=∠DAE≠90°;
乙:AB:AC=AD:AE≠1,∠BAC=∠DAE=90°;
丙:AB:AC=AD:AE≠1,∠BAC=∠DAE≠90°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com