【题目】如图，C，D是以线段AB为直径的⊙O上两点，若CA=CD，且∠ACD=30°，则∠CAB=（ ）
A.15°
B.20°
C.25°
D.30°

（1）则表示 的距离．

（2）数轴上表示x与 7的两点之间的距离可以表示为 .

（3）如果|x-2|=5，则x= .

（4）同理|x+1|+|x-2|表示数轴上有理数x所对应的点到-1和2所对应的点的距离之和，请你找出所有符合条件的整数x，使得|x+1|+|x-2|=3，这样的整数是 .

（5）由以上探索猜想对于任何有理数x，|x+3|+|x-6|的最小值是 .

【题目】二次函数y=ax2+bx+c的图象如图所示，则反比例函数 与一次函数y=bx+c在同一坐标系中的大致图象是（ ）
A.
B.
C.
D.

【题目】将直角边长为6的等腰直角△AOC放在平面直角坐标系中，点O为坐标原点，点C、A分别在x轴，y轴的正半轴上，一条抛物线经过点A、C及点B（﹣3，0）．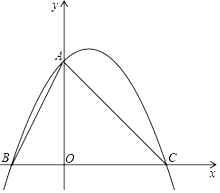

（1）求该抛物线的解析式；
（2）若点P是线段BC上一动点，过点P作AB的平行线交AC于点E，连接AP，当△APE的面积最大时，求点P的坐标；
（3）若点P（t，t）在抛物线上，则称点P为抛物线的不动点，将（1）中的抛物线进行平移，平移后，该抛物线只有一个不动点，且顶点在直线y=2x﹣ 上，求此时抛物线的解析式．

【题目】在△ABC中，∠ACB=30°，将△ABC绕点B按逆时针方向旋转，得到△A1BC1 ．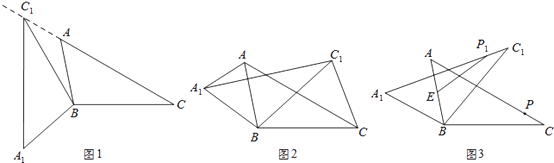

（1）如图1，当点C1在线段CA的延长线时，求∠CC1A1的度数；
（2）已知AB=6，BC=8，
①如图2，连接AA1 ， CC1 ， 若△CBC1的面积为16，求△ABA1的面积；
②如图3，点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转的过程中，点P的对应是点P1 ， 直接写出线段EP1长度的最大值．
（3）线段EP1长度的最大值为11，理由如下：

， -, 0, ,‐3.1415926, 20%, ‐3, 2, -1，3.1010010001…（每两个1之间逐次增加1个0）

①正数集合{ ……}

②负数集合{ ……}

③整数集合{ ……}

④负分数集合{ ……}

⑤无理数集合{ ……}

【题目】计算：（1） （2）

（3） （4）

（5） （6）-14+16÷（-2）3×|-3-1|

【题目】如图，小河上有一拱桥，拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE、ED、DB组成，已知河底ED是水平的，ED=16米，AE=8米，抛物线的顶点C到ED的距离是11米，以ED所在的直线为x轴，抛物线的对称轴为y轴建立平面直角坐标系．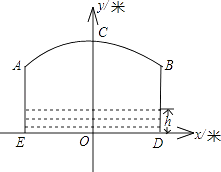
（1）根据题意，填空： ①顶点C的坐标为；
②B点的坐标为；
（2）求抛物线的解析式；
（3）已知从某时刻开始的40小时内，水面与河底ED的距离h（单位：米）随时间t（单位：时）的变化满足函数关系h=﹣ （t﹣19）2+8（0≤t≤40），且当点C到水面的距离不大于5米时，需禁止船只通行，请通过计算说明：在这一时段内，需多少小时禁止船只通行？