（1）求证：四边形ADCE是矩形；

（2）当△ABC满足什么条件时，四边形ADCE是正方形？给出证明.

（1）若AB=12 cm，则MN的长度是______cm；

（2）若AC=3 cm，CP=1 cm，求线段PN的长度．

（1）求证：四边形PMEN是平行四边形；

（2） 当AP为何值时，四边形PMEN是菱形？并给出证明。

【题目】如图，在数轴上有A、B、C、D四个整数点（即各点均表示整数），且2AB=BC=3CD，若A、D两点表示的数分别为﹣5和6，且AC的中点为E，BD的中点为M，BC之间距点B的距离为BC的点N，则该数轴的原点为（　　）

A. 点E B. 点F C. 点M D. 点N

【题目】在平面直角坐标系中，直线与轴、轴分别交于点、点，与双曲线 交于、两点，分别过点、点作轴，轴，垂足分别为点、点，

（1）求线段的长；

（2）若．

①求直线的解析式；

②请你判断线段与线段的大小关系，并说明理由.

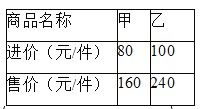
【题目】某商场同时购进甲、乙两种商品共件，其进价和售价如右表，设其中甲种商品购进件．

（1）直接写出购进乙种商品的件数；（用含的代数式表示）

（2）若设该商场售完这件商品的总利润为元．

①求与的函数关系式；

②该商品计划最多投入元用于购买这两种商品，则至少要购进多少件甲商品？若售完这些商品，则商场可获得的最大利润是多少元？

【题目】观察下列两个等式：2﹣＝2×+1，5﹣＝5×+1，给出定义如下：我们称使等式a﹣b＝ab+1的成立的一对有理数a，b为“共生有理数对”，记为（a，b），如：数对（2，），（5，），都是“共生有理数对”．

（1）数对（﹣2，1），（3，）中是“共生有理数对”的是　 　；

（2）若（m，n）是“共生有理数对”，则（﹣n，﹣m）　 　“共生有理数对”（填“是”或“不是”）；

（3）请再写出一对符合条件的“共生有理数对”为　 　；（注意：不能与题目中已有的“共生有理数对”重复）

（4）若（a，3）是“共生有理数对”，求a的值．

(1)求手机支付金额y(元)与骑行时间x(时)的函数关系式；

(2)李老师经常骑行共享单车，请根据不同的骑行时间帮他确定选择哪种支付方式比较合算．

【题目】如图，点E是正方形ABCD的边DC上一点，把△ADE顺时针旋转△ABF的位置．

（1）旋转中心是点 ， 旋转角度是度；
（2）若连结EF，则△AEF是三角形；并证明；
（3）若四边形AECF的面积为25，DE=2，求AE的长．