（1）求1+3+32+33+34+35+36的值；

（2）求1+a+a2+a3+…+a2013（a≠0且a≠1）的值．

【题目】如图，已知△ABC是等边三角形，以AB为直径作⊙O，交BC边于点D，交AC边于点F，作DE⊥AC于点E．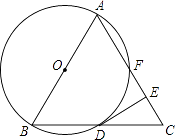

（1）求证：DE是⊙O的切线；
（2）若△ABC的边长为4，求EF的长度．

从表可知，
①抛物线与x轴的交点为；
②抛物线的对称轴是；
③函数y=ax2+bx+c的最大值为；
④x ， y随x增大而增大．

【题目】射线QN与等边△ABC的两边AB，BC分别交于点M，N，且AC∥QN，AM=MB=2cm，QM=4cm．动点P从点Q出发，沿射线QN以每秒1cm的速度向右移动，经过t秒，以点P为圆心， cm为半径的圆与△ABC的边相切（切点在边上），请写出t可取的一切值（单位：秒）

【题目】如图，在扇形OAB中，∠AOB=90°，OA=3，将扇形OAB绕点A逆时针旋转n°（0＜n＜180）后得到扇形O′AB′，当点O在弧AB′上时，n为 ， 图中阴影部分的面积为 ．

饮水问题是关系到学生身心健康的重要生活环节,东坡中学共有教学班24个,平均每班有学生50人,经估算,学生一年在校时间约为240天(除去各种节假日),春、夏、秋、冬季各60天.原来,学生饮水一般都是购纯净水(其他碳酸饮料或果汁价格更高),纯净水零售价为1.5元/瓶,每个学生春、秋、冬季平均每天买1瓶纯净水,夏季平均每天要买2瓶纯净水,学校为了减轻学生消费负担,要求每个班自行购买1台冷热饮水机,经调查,购买一台功率为500 W的冷热饮水机约为150元,纯净水每桶6元,每班春、秋两季,平均每1.5天购买4桶,夏季平均每天购买5桶,冬季平均每天购买1桶,饮水机每天开10小时,当地民用电价为0.50元/度.

问题:

(1)在未购买饮水机之前,全年平均每个学生要花费多少钱来购买纯净水饮用?

(2)在购买饮水机解决学生饮水问题后,每班当年共要花费多少元?

(3)这项便利学生的措施实施后,东坡中学当年全体学生共节约多少钱?

（1）求这款电动车每台的进价？（利润率==）．

（2）在这次促销活动中，商场销售了这款电动车100台，问盈利多少元？

（1）请写出与A，B两点距离相等的点M所对应的数　 　．

（2）现有一只电子蚂蚁P从B点出发，以6单位/秒的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以4单位/秒的速度向右运动，x秒后两只电子蚂蚁在数轴上的C点相遇，请列方程求出x，并指出点C表示的数．

（3）若当电子蚂蚁P从B点出发时，以6单位/秒的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以4单位/秒的速度也向左运动，y秒后两只电子蚂蚁在数轴上的D点相遇，请列方程求出y并指出点D表示的数．

【题目】如图，在大小为4×4的正方形网格中，是相似三角形的是（请填上编号）．