
科目: 来源: 题型:
【题目】某工厂一周计划每日生产某产品100吨,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为正数,减少的吨数记为负数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减/吨 | ﹣1 | +3 | ﹣2 | +4 | +7 | ﹣5 | ﹣10 |
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)本周总生产量是多少吨?比原计划增加了还是减少了?增减数为多少吨?
(3)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?(结果精确到0.01吨)
查看答案和解析>>
科目: 来源: 题型:
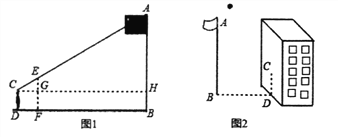
【题目】数学兴趣小组测量校园内旗杆的高度,有以下两种方案:
方案一:小明在地面上直立一根标杆![]() ,沿着直线
,沿着直线![]() 后退到点
后退到点![]() ,使眼睛
,使眼睛![]() 、标杆的顶点
、标杆的顶点![]() 、旗杆的顶点
、旗杆的顶点![]() 在同一直线上(如图1).测量:人与标杆的距离
在同一直线上(如图1).测量:人与标杆的距离![]() =1 m,人与旗杆的距离
=1 m,人与旗杆的距离![]() =16m,人的目高和标杆的高度差
=16m,人的目高和标杆的高度差![]() =0.9m,人的高度
=0.9m,人的高度![]() =1.6m.
=1.6m.
方案二:小聪在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米(如图2).
请你结合上述两个方案,选择其中的一个方案求旗杆的高度。我选择方案 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
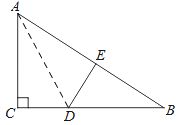
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】观察下列各等式:
13=1=![]() ×11×22
×11×22
13+23=9=![]() ×22×32
×22×32
13+23+33=36=![]() ×32×42
×32×42
…
用你发现的规律解答下列问题:
(1)填空:13+23+33+…+(n﹣1)3+n3=![]() ×( )2×( )2(n为正整数);
×( )2×( )2(n为正整数);
(2)计算:
①13+23+33+…+493+503;
②23+43+63+…+983+1003
查看答案和解析>>
科目: 来源: 题型:
【题目】已知A=2a2+3ab﹣2a﹣1,B=﹣a2+![]() ab+
ab+![]() .
.
(1)a=﹣1,b=﹣2时,求4A﹣(3A﹣2B)的值;
(2)若(1)中式子的值与a的取值无关,求b的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 的面积为9,点
的面积为9,点![]() 在
在![]() 的边上运动.作点
的边上运动.作点![]() 关于原点
关于原点![]() 的对称点
的对称点![]() ,再以
,再以![]() 为边作等边
为边作等边![]() .当点
.当点![]() 在
在![]() 的边上运动一周时,点
的边上运动一周时,点![]() 随之运动所形成的图形面积为( )
随之运动所形成的图形面积为( )

A. 3 B. 9 C. 27 D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在数轴上,点A、B表示的数分别是有理数a,b.
(1)若点A在原点的左侧,点B在原点的右侧,且|a|=|b|,则a与b的关系是 ,用式子表示为 .
(2)若a=﹣5,b=1![]()
①分别写出a,b的相反数;
②求|a![]() |﹣|b
|﹣|b![]() |的值.
|的值.
查看答案和解析>>
科目: 来源: 题型:
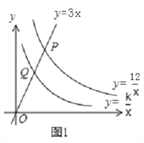
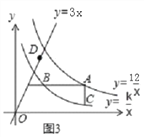
【题目】如图1,已知直线y=3x分别与双曲线y=![]() 、y=
、y=![]() (x>0)交于P、Q两点,且OP=2OQ.
(x>0)交于P、Q两点,且OP=2OQ.
(1)求k的值.
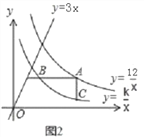
(2)如图2,若点A是双曲线y= ![]() 上的动点,AB∥x轴,AC∥y轴,分别交双曲线y=
上的动点,AB∥x轴,AC∥y轴,分别交双曲线y=![]() (x>0)于点B、C,连接BC.请你探索在点A运动过程中,△ABC的面积是否变化?若不变,请求出△ABC的面积;若改变,请说明理由;
(x>0)于点B、C,连接BC.请你探索在点A运动过程中,△ABC的面积是否变化?若不变,请求出△ABC的面积;若改变,请说明理由;
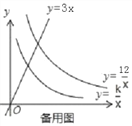
(3)如图3,若点D是直线y=3x上的一点,请你进一步探索在点A运动过程中,以点A、B、C、D为顶点的四边形能否为平行四边形?若能,求出此时点A的坐标;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
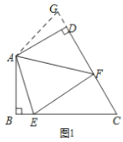
【题目】“半角型”问题探究:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.小明同学的方法是将△ABE绕点A逆时针旋转120°到△ADG的位置,然后再证明△AFE≌△AFG,从而得出结论:EF=BE+DF
(1)如图2,在四边形ABCD中,AB=AD,∠B +∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由.
∠BAD,上述结论是否仍然成立,并说明理由.
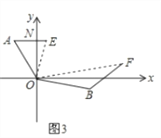
(2)实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离?

拓展提高
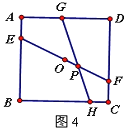
(3)如图4,边长为5的正方形ABCD中,点E、F分别在AB、CD上,AE=CF=1,O为EF的中点,动点G、H分别在边AD、BC上,EF与GH的交点P在O、F之间(与0、F不重合),且∠GPE=45°,设AG=m,求m的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com