
科目: 来源: 题型:
【题目】如图,已知四点A,B,C,D,用圆规和无刻度的直尺按下列要求与步骤画出图形并计算:

(1)画直线AB;
(2)画射线DC;
(3)延长线段DA至点E,使AE=AB;(保留作图痕迹)
(4)画一点P,使点P既在直线AB上,又在线段CE上;
(5)若AB=2cm,AD=1cm,求线段DE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,等边三角形纸片ABC中,点D在边AB(不包含端点A、B)上运动,连接CD,将∠ADC对折,点A落在直线CD上的点A′处,得到折痕DE;将∠BDC对折,点B落在直线CD上的点B′处,得到折痕DF.
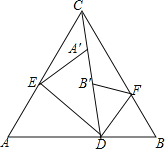
(1)若∠ADC=80°,求∠BDF的度数;
(2)试问∠EDF的大小是否会随着点D的运动而变化?若不变,求出∠EDF的大小;若变化,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】若点A、B、C在数轴上对应的数分别为a、b、c满足|a+5|+|b-1|+|c-2|=0.
(1)在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,请说明理由;
(2)若点A,B,C同时开始在数轴上分别以每秒1个单位长度,每秒3个单位长度,每秒5个单位长度沿着数轴负方向运动.经过t(t≥1)秒后,试问AB-BC的值是否会随着时间t的变化而变化?请说明理由.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,正中设计一个圆形喷水池,若四周圆形和中间圆形的半径均为![]() 米,广场长为
米,广场长为![]() 米,宽为
米,宽为![]() 米.
米.
(1)请列式表示广场空地的面积;
(2)若休闲广场的长为500米,宽为300米,圆形花坛的半径为20米,求广场空地的面积(计算结果保留![]() ).
).

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在射线BA,BC,AD,CD围成的菱形ABCD中,∠ABC=60°,AB=6 ![]() ,O是射线BD上一点,⊙O与BA,BC都相切,与BO的延长线交于点M.过M作EF⊥BD交线段BA(或射线AD)于点E,交线段BC(或射线CD)于点F.以EF为边作矩形EFGH,点G,H分别在围成菱形的另外两条射线上.
,O是射线BD上一点,⊙O与BA,BC都相切,与BO的延长线交于点M.过M作EF⊥BD交线段BA(或射线AD)于点E,交线段BC(或射线CD)于点F.以EF为边作矩形EFGH,点G,H分别在围成菱形的另外两条射线上. 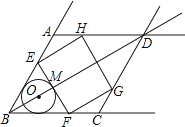
(1)求证:BO=2OM.
(2)设EF>HE,当矩形EFGH的面积为24 ![]() 时,求⊙O的半径.
时,求⊙O的半径.
(3)当HE或HG与⊙O相切时,求出所有满足条件的BO的长.
查看答案和解析>>
科目: 来源: 题型:
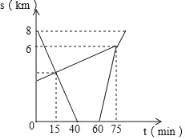
【题目】小刘从家里骑自行车出发,去镇上超市途中碰到妹妹甜甜走路从镇上回家,小刘在超市买完东西回家,在回去的路上又碰到了甜甜,便载甜甜一起回家,结果小刘比正常速度回家的时间晚了3分钟,二人离镇的距离S(千米)和小刘从家出发后的时间t(分钟)之间的关系如图所示,(假设二人之间交流时间忽略不计)
(1)小刘家离镇上的距离 .
(2)小刘和甜甜第1次相遇时离镇上距离是多少?
(3)小刘从家里出发到回家所用的时间?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=x2﹣mx﹣3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.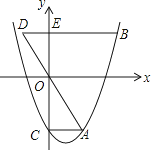
(1)用含m的代数式表示BE的长.
(2)当m= ![]() 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com