【题目】如图，在ABCD中，P是CD边上一点，且AP和BP分别平分∠DAB和∠CBA，若AD=5，AP=8，则△APB的周长是 ．

（1）求证：CE=CF；

（2）若点G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？

【题目】两个小组同时从甲地出发，匀速步行到乙地，甲乙两地相距7500米，第一组的步行速度是第二组的1.2倍，并且比第二组早15分钟到达乙地．设第二组的步行速度为x千米/小时，根据题意可列方程是（　　）
A.﹣ =15
B.﹣ =
C.﹣ =15
D.﹣ =

（1）请直接写出点B关于点A对称的点的坐标；

（2）将△ABC绕坐标原点O逆时针旋转90°，画出图形，直接写出点B的对应点的坐标；

（3）请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标．

【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论中正确的是（　　）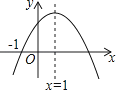

A.a＞0
B.c＜0
C.3是方程ax2+bx+c=0的一个根
D.当x＜1时，y随x的增大而减小

（1）根据小明的解答（图1）将下列各式因式分解

①a2-12a+20

②（a-1）2-8（a-1）+7

③a2-6ab+5b2

（2）根据小丽的思考（图2）解决下列问题．

①说明：代数式a2-12a+20的最小值为-16．

②请仿照小丽的思考解释代数式-（a+1）2+8的最大值为8，并求代数式-a2+12a-8的最大值．

如图，在△ABC中，已知∠ADE＝∠B，∠1＝∠2，FG⊥AB于点G.

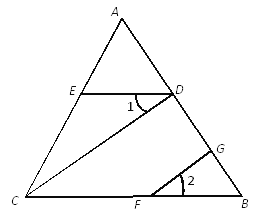
求证CD⊥AB.

证明:∵∠ADE＝∠B（已知），

∴ （ ），

∵ DE∥BC（已证），

∴ （ ），

又∵∠1＝∠2（已知），

∴ （ ），

∴CD∥FG（ ），

∴ （两直线平行同位角相等），

∵ FG⊥AB（已知），

∴∠FGB＝90°（垂直的定义）.

即∠CDB＝∠FGB＝90°，

∴CD⊥AB. （垂直的定义）.

（1）根据特征画出平移后的△A′B′C′；

（2）利用网格的特征，画出AC边上的高BE并标出画法过程中的特征点；

（3）△A′B′C′的面积为 ．

（1）如图1，若DE平分∠ADC，BF平分∠ABC的邻补角，判断DE与BF位置关系并证明．

（2）如图2，若BF、DE分别平分∠ABC、∠ADC的邻补角，判断DE与BF位置关系并证明．