
科目: 来源: 题型:
【题目】如图,在ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( ) 
A.1:3
B.1:5
C.1:6
D.1:11
查看答案和解析>>
科目: 来源: 题型:
【题目】小红同学四次中考数学模拟考试成绩分别是:96,104,104,116,关于这组数据下列说法错误的是( )
A.平均数是105
B.众数是104
C.中位数是104
D.方差是50
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣x+4与x轴、y轴分别交于点A、B,抛物线y=﹣ ![]() (x﹣m)2+n的顶点P在直线y=﹣x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.
(x﹣m)2+n的顶点P在直线y=﹣x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.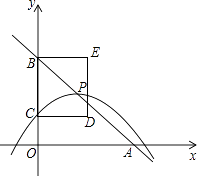
(1)n=(用含m的代数式表示),点C的纵坐标是(用含m的代数式表示);
(2)当点P在矩形BCDE的边DE上,且在第一象限时,求抛物线对应的函数解析式;
(3)直接写出矩形BCDE有两个顶点落在抛物线上时m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎.该打车方式的计价规则如图①所示,若车辆以平均速度vkm/h行驶了skm,则打车费用为(ps+60q·![]() )元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.
)元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.
(1)当x≥6时,求y与x的函数关系式.
(2)若p=1,q=0.5,求该车行驶的平均速度.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,直线EF分别交两直角边AB、BC与E、F两点,且EF∥AC,P是斜边AC的中点,连接PE,PF,且AB= ![]() ,BC=
,BC= ![]() .
.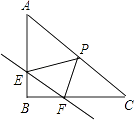
(1)当E、F均为两直角边的中点时,求证:四边形EPFB是矩形,并求出此时EF的长;
(2)设EF的长度为x(x>0),当∠EPF=∠A时,用含x的代数式表示EP的长;
(3)设△PEF的面积为S,则当EF为多少时,S有最大值,并求出该最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y=![]() 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.
(1)求反比例函数和一次函数的解析式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知点D,E分别在AB,AC上,要使DE∥BC,必须具备哪些条件?尽可能把所有条件写出来。

比如:
(1)如果∠DEC+∠ECB=180°,那么DE∥BC:
(2)_________________________________;
(3)_________________________________;
(4)_________________________________;
(5)__________________________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平面直角坐标系中,矩形OABC的一边OA在x轴上,B点的坐标为(4,3).双曲线y= ![]() (x>0)过BC的中点P,交AB于点Q.
(x>0)过BC的中点P,交AB于点Q. 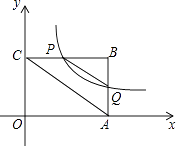
(1)求双曲线的函数表达式及点Q的坐标;
(2)判断线段AC与线段PQ之间的关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校九年级学生举行朗诵比赛,全年级学生都参加,学校对表现优异的学生进行表彰,设置一、二、三等奖各进步奖共四个奖项,赛后将九年级(1)班的获奖情况绘制成如图所示的两幅不完整的统计图,请根据图中的信息,解答下列问题: 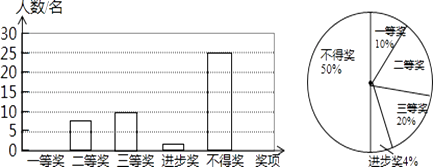
(1)九年级(1)班共有名学生;
(2)将条形图补充完整:在扇形统计图中,“二等奖”对应的扇形的圆心角度数是;
(3)如果该九年级共有1250名学生,请估计荣获一、二、三等奖的学生共有多少名.
查看答案和解析>>
科目: 来源: 题型:
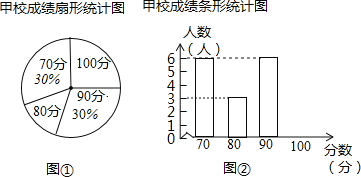
【题目】某市团委举行以“我的中国梦”为主题的知识竞赛,甲、乙两所学校的参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如图不完整的统计图表:
乙校成绩统计表 | |
分数 | 人数 |
70 | 7 |
80 | ______ |
90 | 1 |
100 | 8 |
![]() 乙学校的参赛人数是______人
乙学校的参赛人数是______人![]()
![]() 在图
在图![]() 中,“80分”所在扇形的圆心角度数为______;
中,“80分”所在扇形的圆心角度数为______;
![]() 请你将图
请你将图![]() 补充完整;
补充完整;
![]() 求乙校成绩的平均分.
求乙校成绩的平均分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com