
科目: 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),该抛物线的对称轴为直线x=﹣1,若点C(﹣ ![]() ,y1),D(﹣
,y1),D(﹣ ![]() ,y2),E(
,y2),E( ![]() ,y3)均为函数图象上的点,则y1 , y2 , y3的大小关系为 .
,y3)均为函数图象上的点,则y1 , y2 , y3的大小关系为 . 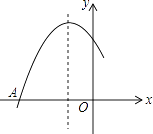
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,等边△ABC的边长为3,F为BC边上的动点,FD⊥AB于D,FE⊥AC于E,则DE的长为( )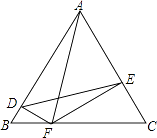
A.随F点运动,其值不变
B.随F点运动而变化,最大值为 ![]()
C.随F点运动而变化,最小值为 ![]()
D.随F点运动而变化,最小值为 ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab.
又∵S四边形ADCB=S△ADB+S△DCB= 12 c2+ 12 a(b﹣a)
∴ 12 b2+ 12 ab= 12 c2+ 12 a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .

查看答案和解析>>
科目: 来源: 题型:
【题目】对于抛物线y=ax2﹣4ax+3a下列说法:①对称轴为x=2;②抛物线与x轴两交点的坐标分别为(1,0),(3,0);③顶点坐标为(2,﹣a);④若a<0,当x>2时,函数y随x的增大而增大,其中正确的结论有( )个.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目: 来源: 题型:
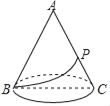
【题目】如图,圆锥的轴截面是边长为6cm的正三角形ABC,P是母线AC的中点,则在圆锥的侧面上从B点到P点的最短路线的长为( )
A. ![]() B. 2
B. 2![]() C. 3
C. 3![]() D. 4
D. 4![]()
查看答案和解析>>
科目: 来源: 题型:
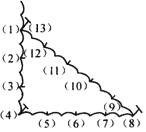
【题目】古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )
A. 直角三角形两个锐角互补
B. 三角形内角和等于180°
C. 如果三角形两条边长的平方和等于第三边长的平方
D. 如果三角形两条边长的平方和等于第三边长的平方,那么这个三角形是直角三角形
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在同一平面内,将△ABC绕点A旋转到△AED的位置,若AE⊥BC,∠ADC=65°,则∠ABC的度数为( )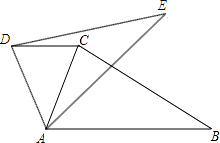
A.30°
B.40°
C.50°
D.60°
查看答案和解析>>
科目: 来源: 题型:
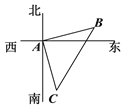
【题目】如图,在一次测绘活动中,某同学站在点A处观测停放于B、C两处的小船,测得船B在点A北偏东75°方向150米处,船C在点A南偏东15°方向120米处,则船B与船C之间的距离为______米(精确到0.1![]() ).
).
查看答案和解析>>
科目: 来源: 题型:
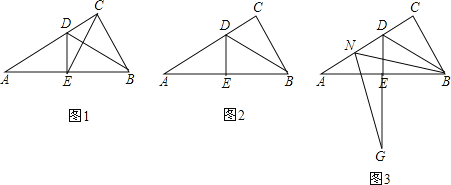
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.
(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.求证:AD=DG+MD;
(3)点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.请在图3中画出图形,并直接写出ND,DG与AD数量之间的关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:我们把平面内与一个定点F和一条定直线l(l不经过点F)距离相等的点的轨迹(满足条件的所有点所组成的图形)叫做抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线.
(1)已知抛物线的焦点F(0, ![]() ),准线l:
),准线l: ![]() ,求抛物线的解析式;
,求抛物线的解析式;
(2)已知抛物线的解析式为:y=x2﹣n2 , 点A(0, ![]() )(n≠0),B(1,2﹣n2),P为抛物线上一点,求PA+PB的最小值及此时P点坐标;
)(n≠0),B(1,2﹣n2),P为抛物线上一点,求PA+PB的最小值及此时P点坐标;
(3)若(2)中抛物线的顶点为C,抛物线与x轴的两个交点分别是D、E,过C、D、E三点作⊙M,⊙M上是否存在定点N?若存在,求出N点坐标并指出这样的定点N有几个;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com