
科目: 来源: 题型:
【题目】如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4, 
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是某超市地下停车场入口的设计图,请根据图中数据计算CE的长度.(结果保留小数点后两位;参考数据:sin22°=0.3746,cos22°=0.9272,tan22°=0.4040)
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,已知反比例函数y= ![]() 的图象经过点A,点O是坐标原点,OA=2且OA与x轴的夹角是60°.
的图象经过点A,点O是坐标原点,OA=2且OA与x轴的夹角是60°. 
(1)试确定此反比例函数的解析式;
(2)将线段OA绕O点顺时针旋转30°得到线段OB,判断点B是否在此反比例函数的图象上,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】为践行党的群众路线,六盘水市教育局开展了大量的教育教学实践活动,如图是其中一次“测量旗杆高度”的活动场景抽象出的平面几何图形.
活动中测得的数据如下:
①小明的身高DC=1.5m
②小明的影长CE=1.7cm
③小明的脚到旗杆底部的距离BC=9cm
④旗杆的影长BF=7.6m
⑤从D点看A点的仰角为30°
请选择你需要的数据,求出旗杆的高度.(计算结果保留到0.1,参考数据 ![]() ≈1.414.
≈1.414. ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目: 来源: 题型:
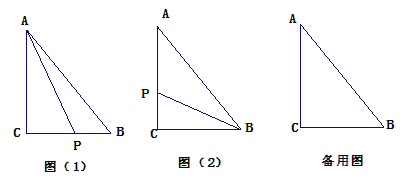
【题目】如图(1)在△ABC中,∠C=90°,AB=25cm,BC=15cm,若动点P从点C开始沿着C→B→A→C的路径运动,且速度为每秒5cm,设点P运动的时间为t秒.
(1)点P运动2秒后,求△ABP的面积;
(2)如图(2),当t为何值时,BP平分∠ABC;
(3)当△BCP为等腰三角形时,直接写出所有满足条件t的值.
查看答案和解析>>
科目: 来源: 题型:
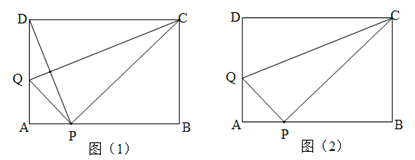
【题目】如图(1)将长方形纸片ABCD的一边CD沿着CQ向下折叠,使点D落在边AB上的点P处.
(1)试判断线段CQ与PD的关系,并说明理由;
(2)如图(2),若AB=CD=5,AD=BC=3.求AQ的长;
(3)如图(2),BC=3,取CQ的中点M,连接MD,PM,若MD⊥PM,求AQ(AB+BC)的值.
查看答案和解析>>
科目: 来源: 题型:
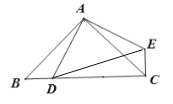
【题目】如图,在△ABC中,∠BAC=90°,AC=AB,点D为BC边上的一个动点(点D不与B,C重合),以AD为边作等腰直角△ADE,∠DAE=90°,连接CE.
(1)求证:△ABD≌△ACE.
(2)试猜想线段BD,CD,DE之间的等量关系,并证明你的猜想.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知直线![]() ,点
,点![]() 在直线
在直线![]() 上,点
上,点![]() 到直线
到直线![]() 的距离分别为1,2.
的距离分别为1,2.
(1)利用直尺和圆规作出以![]() 为底的等腰△ABC,使点
为底的等腰△ABC,使点![]() 在直线
在直线![]() 上(保留作图痕迹,不写作法).
上(保留作图痕迹,不写作法).
(2)若(1)中得到的△ABC为等腰直角三角形,求△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com