
科目: 来源: 题型:
【题目】小王家距上班地点18千米,他用乘公交车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程的2倍还多9千米.他从家出发到达上班地点,乘公交车方式所用时间是自驾车方式所用时间的![]() .小王用自驾车方式上班平均每小时行驶( )
.小王用自驾车方式上班平均每小时行驶( )
A. 26千米 B. 27千米 C. 28千米 D. 30千米
查看答案和解析>>
科目: 来源: 题型:
【题目】(问题探究)
(1)如图①已知锐角△ABC,分别以AB、AC为腰,在△ABC的外部作等腰Rt△ABD和Rt△ACE,连接CD、BE,是猜想CD、BE的大小关系_____________ ;(不必证明)
(深入探究)
(2)如图②△ABC、△ADE都是等腰直角三角形,点D在边BC上(不与B、C重合),连接EC,则线段 BC,DC,EC 之间满足的等量关系式为________________ ;(不必证明) 线段 AD2,BD2,CD2之间满足的等量关系,并证明你的结论;
(拓展应用)
(3)如图③,在四边形 ABCD 中,∠ABC=∠ACB=∠ADC=45°.若 BD=9,CD=3,
求 AD 的长.

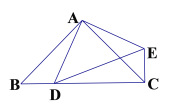

① ② ③
查看答案和解析>>
科目: 来源: 题型:
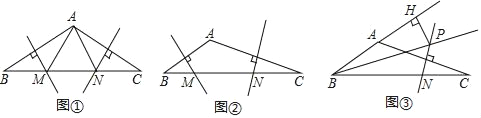
【题目】在△ABC中,AB、AC边的垂直平分线分别交BC边于点M、N.
(1)如图①,若△AMN是等边三角形,则∠BAC= °;
(2)如图②,若∠BAC=135°,求证:BM2+CN2=MN2.
(3)如图③,∠ABC的平分线BP和AC边的垂直平分线相交于点P,过点P作PH垂直BA的延长线于点H.若AB=4,CB=10,求AH的长.
查看答案和解析>>
科目: 来源: 题型:
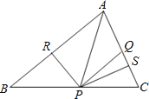
【题目】如图,在△ABC中,点P是BC上一点,PR⊥AB,PS⊥AC,垂足分别为点R、S,PR=PS,点Q是AC上一点,且AQ=PQ,
(1)求证:QP∥AR;
(2)AR、AS相等吗?说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在等腰梯形ABCD中,∠B=60°,P、Q同时从B出发,以每秒1个单位长度分别沿B→A→D→C和B→C→D方向运动至相遇时停止.设运动时间为t(秒),△BPQ的面积为S(平方单位),S与t的函数图象如图2,则下列结论错误的是( )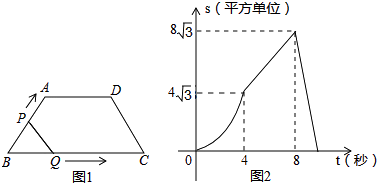
A.当t=4秒时,S=4 ![]()
B.AD=4
C.当4≤t≤8时,S=2 ![]() t
t
D.当t=9秒时,BP平分梯形ABCD的面积
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AC=21,BC=13,D是AC边上一点,BD=12,AD=16,
(1)若E是边AB的中点,求线段DE的长
(2)若E是边AB上的动点,求线段DE的最小值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数是( ) 
A.70°
B.35°
C.40°
D.50°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com