
科目: 来源: 题型:
【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?
(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.请问至少需要补充多少名新工人?
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行八百米跑体能测试,测试结果分为A、B、C、D四个等级,请根据两幅统计图中的信息回答下列问题: 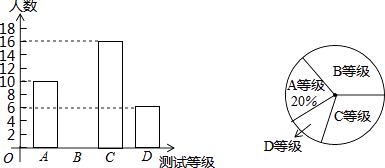
(1)求本次测试共调查了多少名学生?
(2)求本次测试结果为B等级的学生数,并补全条形统计图;
(3)若该中学八年级共有900名学生,请你估计八年级学生中体能测试结果为D等级的学生有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点F在边AC上,并且CF=1,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 . 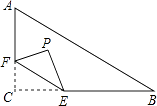
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AB=BC=2 ![]() ,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )
,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( ) 
A.2
B.![]()
C.![]()
D.3
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( ) 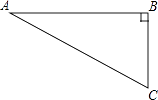
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连接MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.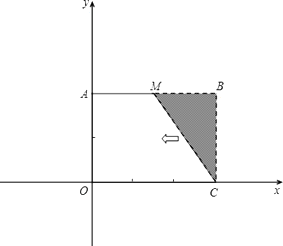
(1)试直接写出点D的坐标;
(2)已知点B与点D在经过原点的抛物线上,点P在第一象限内的该抛物线上移动,过点P作PQ⊥x轴于点Q,连接OP.
①若以O、P、Q为顶点的三角形与△DAO相似,试求出点P的坐标;
②试问在抛物线的对称轴上是否存在一点T,使得|TO﹣TB|的值最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】【问题引入】 已知:如图BE、CF是△ABC的中线,BE、CF相交于G.求证: ![]() =
= ![]() =
= ![]()

证明:连结EF
∵E、F分别是AC、AB的中点
∴EF∥BC且EF= ![]() BC
BC
∴ ![]() =
= ![]() =
= ![]() =
= ![]()
【思考解答】
(1)连结AG并延长AG交BC于H,点H是否为BC中点(填“是”或“不是”)
(2)①如果M、N分别是GB、GC的中点,则四边形EFMN 是四边形. ②当 ![]() 的值为时,四边形EFMN 是矩形.
的值为时,四边形EFMN 是矩形.
③当 ![]() 的值为时,四边形EFMN 是菱形.
的值为时,四边形EFMN 是菱形.
④如果AB=AC,且AB=10,BC=16,则四边形EFMN的面积S= .
查看答案和解析>>
科目: 来源: 题型:
【题目】张师傅驾车运送荔枝到某地出售,汽车出发前油箱有油50升,行驶若干小时后,图中在加油站加油若干升,油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示. 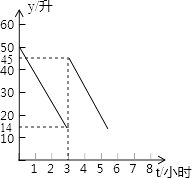
(1)汽车行驶小时后加油,中途加油升;
(2)求加油前油箱剩余油量y与行驶时间t的函数关系式;
(3)已知加油前、后汽车都以70千米/小时匀速行驶,如果加油站距目的地210千米,要到达目的地,问油箱中的油是否够用?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com