
科目: 来源: 题型:
【题目】设a1 , a2 , …,a2014是从1,0,﹣1这三个数中取值的一列数,若a1+a2+…+a2014=69,(a1+1)2+(a2+1)2+…+(a2014+1)2=4001,则a1 , a2 , …,a2014中为0的个数是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=( ) 
A.![]()
B.![]()
C.![]()
D.![]() ﹣2
﹣2
查看答案和解析>>
科目: 来源: 题型:
【题目】我们知道平行四边形那有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论
(1)【发现与证明】
在ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′D.
结论1:B′D∥AC;
结论2:△AB′C与ABCD重叠部分的图形是等腰三角形.
…
请利用图1证明结论1或结论2.
(2)【应用与探究】
在ABCD中,∠B=30°,将△ABC沿AC翻折至△AB′C,连接B′D.
如图1,若AB= ![]() ,∠AB′D=75°,则∠ACB= , BC=;
,∠AB′D=75°,则∠ACB= , BC=;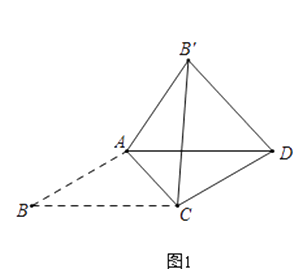
(3)如图2,AB=2 ![]() ,BC=1,AB′与CD相交于点E,求△AEC的面积;
,BC=1,AB′与CD相交于点E,求△AEC的面积;
(4)已知AB=2 ![]() ,当BC的长为多少时,△AB′D是直角三角形?
,当BC的长为多少时,△AB′D是直角三角形?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,点M为抛物线y=﹣x2+2nx﹣n2+2n的顶点,过点(0,4)作x轴的平行线,交抛物线于点P、Q(点P在Q的左侧),PQ=4.
(1)求抛物线的函数关系式,并写出点P的坐标;
(2)小丽发现:将抛物线y=﹣x2+2nx﹣n2+2n绕着点P旋转180°,所得新抛物线的顶点恰为坐标原点O,你认为正确吗?请说明理由;
(3)如图2,已知点A(1,0),以PA为边作矩形PABC(点P、A、B、C按顺时针的方向排列), ![]() .
.
写出C点的坐标:C( , )(坐标用含有t的代数式表示);
(4)若点C在题(2)中旋转后的新抛物线上,求t的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB. 
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,求证:以A、B、C为顶点的三角形与△AEF相似;
(3)已知AF=4,CF=2.在(2)条件下,求AE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】六一儿童节,小文到公园游玩.看到公园的一段人行弯道MN(不计宽度),如图,它与两面互相垂直的围墙OP、OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等,比如:A、B、C是弯道MN上的三点,矩形ADOG、矩形BEOH、矩形CFOI的面积相等.爱好数学的他建立了平面直角坐标系(如图),图中三块阴影部分的面积分别记为S1、S2、S3 , 并测得S2=6(单位:平方米).OG=GH=HI. 
(1)求S1和S3的值;
(2)设T(x,y)是弯道MN上的任一点,写出y关于x的函数关系式;
(3)公园准备对区域MPOQN内部进行绿化改造,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,小明从点A处出发,沿着坡角为α的斜坡向上走了0.65千米到达点B,sinα= ![]() ,然后又沿着坡度为i=1:4的斜坡向上走了1千米达到点C.问小明从A点到点C上升的高度CD是多少千米(结果保留根号)?
,然后又沿着坡度为i=1:4的斜坡向上走了1千米达到点C.问小明从A点到点C上升的高度CD是多少千米(结果保留根号)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com