【题目】如图，已知△ABC中，AB=AC，O为BC的中点，AB与⊙O相切于点D．

（1）求证：AC是⊙O的切线；
（2）若∠B=33°，⊙O的半径为1，求BD的长．（结果精确到0.01）

【题目】某蔬菜生产基地在气温较低时，用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种，下图是某天恒温系统从开启到关闭及关闭后，大棚内温度y（℃）随时间x（小时）变化的函数图象，其中BC段是双曲线y= 的一部分．请根据图中信息解答下列问题：

（1）恒温系统在这天保持大棚内温度18℃的时间有多少小时？
（2）求k的值；
（3）当x=18时，大棚内的温度约为多少度？

【题目】如图，已知抛物线y=﹣ x2+mx+n与x轴交于A （﹣2，0）、B两点，与y轴交于点C．抛物线对称轴为直线x=3，且对称轴与x轴交于点D．

（1）求抛物线的解析式；
（2）点P在线段BC上从点C开始向点B运动（点P不与点B、C重合），速度为每秒 个单位，设运动时间为t（单位：s），过点P作x轴的垂线与抛物线相交于点F．求四边形CDBF的面积S关于t的函数关系式．

【题目】如图1，在△ABC中，CD为AB边上的中线，点E、F分别在线段CD、AD上，且 ．点G是EF的中点，射线DG交AC于点H．

（1）求证：△DFE∽△DAC；
（2）请你判断点H是否为AC的中点？并说明理由；
（3）若将△ADH绕点D顺时针旋转至△A′DH′，使射线DH′与射线CB相交于点M（不与B，C重合．图2是旋转后的一种情形），请探究∠BMD与∠BDA′之间所满足的数量关系，并加以证明．

【题目】直线y= x+2 与x轴，y轴分别交于M，N两点，O为坐标原点，将△OMN沿直线MN翻折后得到△PMN，则点P的坐标为 ．

【题目】如图，以A点为圆心，以相同的长为半径作弧，分别与射线AM，AN交于B，C两点，连接BC，再分别以B，C为圆心，以相同长（大于 BC）为半径作弧，两弧相交于点D，连接AD，BD，CD．则下列结论错误的是（ ）

A.AD平分∠MAN
B.AD垂直平分BC
C.∠MBD=∠NCD
D.四边形ACDB一定是菱形

【题目】如图，⊙O的弦BC长为8，点A是⊙O上一动点，且∠BAC=45°，点D，E分别是BC，AB的中点，则DE长的最大值是（ ）

A.4
B.4
C.8
D.8

【题目】如图，在△ABC中，AB=5，AC=9，S△ABC= ，动点P从A点出发，沿射线AB方向以每秒5个单位的速度运动，动点Q从C点出发，以相同的速度在线段AC上由C向A运动，当Q点运动到A点时，P、Q两点同时停止运动，以PQ为边作正方形PQEF（P、Q、E、F按逆时针排序），以CQ为边在AC上方作正方形QCGH．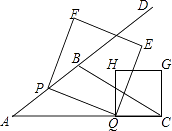

（1）求tanA的值；
（2）设点P运动时间为t，正方形PQEF的面积为S，请探究S是否存在最小值？若存在，求出这个最小值，若不存在，请说明理由；
（3）当t为何值时，正方形PQEF的某个顶点（Q点除外）落在正方形QCGH的边上，请直接写出t的值．

【题目】高铁的开通，给衢州市民出行带来了极大的方便，“五一”期间，乐乐和颖颖相约到杭州市的某游乐园游玩，乐乐乘私家车从衢州出发1小时后，颖颖乘坐高铁从衢州出发，先到杭州火车站，然后再转车出租车去游乐园（换车时间忽略不计），两人恰好同时到达游乐园，他们离开衢州的距离y（千米）与乘车时间t（小时）的关系如图所示． 请结合图象解决下面问题：

（1）高铁的平均速度是每小时多少千米？
（2）当颖颖达到杭州火车东站时，乐乐距离游乐园还有多少千米？
（3）若乐乐要提前18分钟到达游乐园，问私家车的速度必须达到多少千米/小时？

【题目】小明在课外学习时遇到这样一个问题：
定义：如果二次函数y=a1x2+b1x+c1（a1≠0，a1 ， b1 ， c1是常数）与y=a2x2+b2x+c2（a2≠0，a2 ， b2 ， c2是常数）满足a1+a2=0，b1=b2 ， c1+c2=0，则称这两个函数互为“旋转函数”．
求函数y=﹣x2+3x﹣2的“旋转函数”．
小明是这样思考的：由函数y=﹣x2+3x﹣2可知，a1=﹣1，b1=3，c1=﹣2，根据a1+a2=0，b1=b2 ， c1+c2=0，求出a2 ， b2 ， c2 ， 就能确定这个函数的“旋转函数”．
请参考小明的方法解决下面问题：
（1）写出函数y=﹣x2+3x﹣2的“旋转函数”；
（2）若函数y=﹣x2+ mx﹣2与y=x2﹣2nx+n互为“旋转函数”，求（m+n）2015的值；
（3）已知函数y=﹣ （x+1）（x﹣4）的图象与x轴交于点A、B两点，与y轴交于点C，点A、B、C关于原点的对称点分别是A1 ， B1 ， C1 ， 试证明经过点A1 ， B1 ， C1的二次函数与函数y=﹣ （x+1）（x﹣4）互为“旋转函数．”