
科目: 来源: 题型:
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )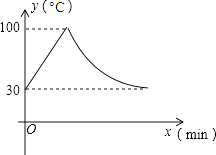
A.7:20
B.7:30
C.7:45
D.7:50
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图①,BP、CP分别平分△ABC的外角∠CBD、∠BCE,BQ、CQ分别平分∠PBC、∠PCB,BM、CN分别是∠PBD、∠PCE的角平分线.
(1)当∠BAC=40°时,∠BPC= ,∠BQC= ;
(2)当BM∥CN时,求∠BAC的度数;
(3)如图②,当∠BAC=120°时,BM、CN所在直线交于点O,直接写出∠BOC的度数.
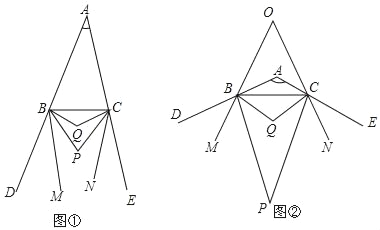
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,以点A为圆心,AB长为半径画弧,交CD于点E,连接AE、BE.作BF⊥AE于点F. 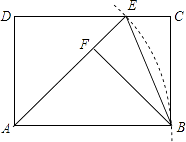
(1)求证:BF=AD;
(2)若EC= ![]() ﹣1,∠FEB=67.5°,求扇形ABE的面积(结果保留π).
﹣1,∠FEB=67.5°,求扇形ABE的面积(结果保留π).
查看答案和解析>>
科目: 来源: 题型:
【题目】小敏在作⊙O的内接正五边形时,先做了如下几个步骤:
(i)作⊙O的两条互相垂直的直径,再作OA的垂直平分线交OA于点M,如图1;
(ii)以M为圆心,BM长为半径作圆弧,交CA于点D,连结BD,如图2.若⊙O的半径为1,则由以上作图得到的关于正五边形边长BD的等式是( )
A.BD2= ![]() OD
OD
B.BD2= ![]() OD
OD
C.BD2= ![]() OD
OD
D.BD2= ![]() OD
OD
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是我国古代计时器“漏壶”的示意图,在壶内盛一定量的水,水从壶底的小孔漏出.壶壁内画有刻度,人们根据壶中水面的位置计时,用x表示时间,y表示壶底到水面的高度,则y与x的函数关系式的图象是( ) 
A.
B.
C.
D.
查看答案和解析>>
科目: 来源: 题型:
【题目】教师运动会中,甲,乙两组教师参加“两人背夹球”往返跑比赛,即:每组两名教师用背部夹着球跑完规定的路程,若途中球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.若距起点的距离用y(米)表示,时间用x(秒)表示.下图表示两组教师比赛过程中y与x的函数关系的图象.根据图象,有以下四个推断:
①乙组教师获胜
②乙组教师往返用时相差2秒
③甲组教师去时速度为0.5米/秒
④返回时甲组教师与乙组教师的速度比是2:3
其中合理的是( )
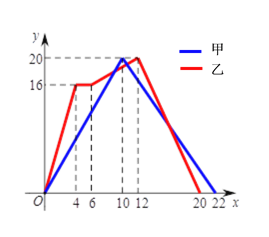
A. ①② B. ①③ C. ②④ D. ①④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,水平面上有一个坡度i=1:2的斜坡AB,矩形货柜DEFG放置在斜坡上,己知DE=2.5m.EF=2m,BF=3.5m,则点D离地面的高DH为 m.(结果保留根号)
查看答案和解析>>
科目: 来源: 题型:
【题目】用n边形的对角线把n边形分割成(n-2)个三角形,共有多少种不同的分割方案(n≥4)?
(探究)为了解决上面的数学问题,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进转化,最后猜想得出结论.不妨假设n边形的分割方案有Pn种.
探究一:用四边形的对角线把四边形分割成2个三角形,共有多少种不同的分割方案?
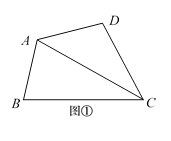
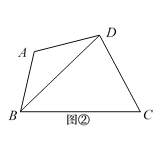
如图①,图②,显然,只有2种不同的分割方案.所以,P4=2.
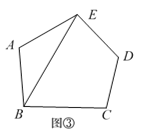
探究二:用五边形的对角线把五边形分割成3个三角形,共有多少种不同的分割方案?
不妨把分割方案分成三类:
第1类:如图③,用A,E与B连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案,所以,此类共有P4种不同的分割方案.
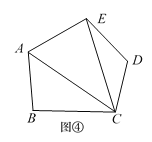
第2类:如图④,用A,E与C连接,把五边形分割成3个三角形,有1种不同的分割方案,可视为![]() 种分割方案.
种分割方案.
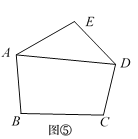
第3类:图⑤,用A,E与D连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案,所以,此类共有P4种不同的分割方案.
所以,P5 =![]() +
+![]() +
+![]() =
=![]() (种)
(种)
探究三:用六边形的对角线把六边形分割成4个三角形,共有多少种不同的分割方案?
不妨把分割方案分成四类:
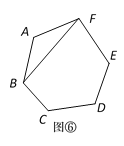
第1类:如图⑥,用A,F与B连接,先把六边形分割转化成1个三角形和1个五边形,再把五边形分割成3个三角形,由探究二知,有P5种不同的分割方案.所以,此类共有P5种不同的分割方案.
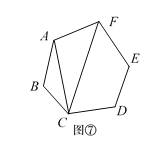
第2类:如图⑦,用A,F与C连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案.所以,此类共有P4种分割方案
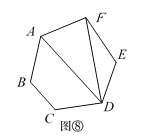
第3类:如图⑧,用A,F与D连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案.所以,此类共有P4种分割方案.
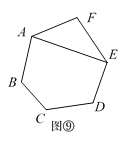
第4类:如图⑨,用A,F与E连接,先把六边形分割转化成1个三角形和1个五边形.再把五边形分割成3个三角形,由探究二知,有P5种不同的分割方案.所以,此类共有P5种分割方案.
所以,P6 =![]() (种)
(种)
探究四:用七边形的对角线把七边形分割成5个三角形,则P7与P6的关系为:
P7 = ![]() ,共有_____种不同的分割方案.……
,共有_____种不同的分割方案.……
(结论)用n边形的对角线把n边形分割成(
(应用)用八边形的对角线把八边形分割成6个三角形,共有多少种不同的分割方案? (应用上述结论,写出解答过程)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,l1和l2分别是走私船和我公安快艇航行路程与时间的函数图象,请结合图象解决下列问题:
(1)在刚出发时,我公安快艇距走私船多少海里?
(2)计算走私船与公安艇的速度分别是多少?
(3)求出l1,l2的解析式.
(4)问6分钟时,走私船与我公安快艇相距多少海里?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com