【题目】如图（1）是一个六角星的纸板，其中六个锐角都为60°，六个钝角都为120°，每条边都相等，现将该纸板按图（2）切割，并无缝隙无重叠地拼成矩形ABCD．若六角星纸板的面积为9 cm2 ， 则矩形ABCD的周长为（ ）
A.18cm
B.8 cm
C.（2 +6）cm
D.（6 +6）cm

【题目】如图，⊙O中，点A为 中点，BD为直径，过A作AP∥BC交DB的延长线于点P．
（1）求证：PA是⊙O的切线；
（2）若 ，AB=6，求sin∠ABD的值．

【题目】圆锥纸帽的侧面展开图是一个圆心角为120°，弧长为6π（cm）的扇形纸片，则圆锥形纸帽的侧面积为（ ）
A.9π cm2
B.18π cm2
C.27π cm2
D.36π cm2

【题目】根据要求完成下列题目：

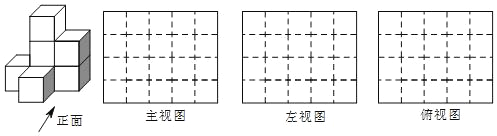
(1)图中有_____块小正方体；

(2)请在下面方格纸中分别画出它的主视图、左视图和俯视图；

(3)用小正方体搭一几何体，使得它的俯视图和左视图与你在图方格中所画的图一致，若这样的几何体最少要m个小正方体，最多要n个小正方体，则m+n的值为____．

【答案】（1）7；（2）画图见解析；（3）16

【解析】

（1）直接根据立体图形得出小正方体的个数；

（2）主视图从左往右小正方形的个数为1，3，2；左视图从左往右小正方形的个数为3，1；俯视图从左往右小正方形的个数1，2，1；

（3）由俯视图易得最底层小立方块的个数，由左视图找到其余层数里最少个数和最多个数相加即可．

（1）图中有7块小正方体；

故答案为：7；

（2）如图所示：

；

（3）用小立方体搭一几何体，使得它的俯视图和左视图与你在上图方格中所画的图一致，则这样的几何体最少要6个小立方块，最多要10个小立方块．则m+n=16

故答案为：16

【点睛】

此题主要考查了三视图，用到的知识点为：三视图分为主视图、左视图、俯视图，分别是从物体正面、左面和上面看，所得到的图形；俯视图决定底层立方块的个数，易错点是由主视图得到其余层数里最少的立方块个数和最多的立方块个数．

【题型】解答题
【结束】
24

（1）过点P画OB的平行线交ON于点M；

（2）过点M画OB的垂线，垂足为H；

（3）度量线段PO、PM与MH的长度，会发现：线段PO与PM的大小关系是 ；线段MH与PM的大小关系是 ．

【题目】某中学在百货商场购进了A、B两种品牌的篮球，购买A品牌篮球花费了2400元，购买B品牌篮球花费了1950元，且购买A品牌篮球数量是购买B品牌篮球数量的2倍，已知购买一个B品牌篮球比购买一个A品牌篮球多花50元．
（1）求购买一个A品牌、一个B品牌的篮球各需多少元？
（2）该学校决定再次购进A、B两种品牌篮球共30个，恰逢百货商场对两种品牌篮球的售价进行调整，A品牌篮球售价比第一次购买时提高了10%，B品牌篮球按第一次购买时售价的9折出售，如果这所中学此次购买A、B两种品牌篮球的总费用不超过3200元，那么该学校此次最多可购买多少个B品牌篮球？

【题目】根据题意解答
（1）【阅读发现】如图①，在正方形ABCD的外侧，作两个等边三角形ABE和ADF，连结ED与FC交于点M，则图中△ADE≌△DFC，可知ED=FC，求得∠DMC= ．
（2）【拓展应用】如图②，在矩形ABCD（AB＞BC）的外侧，作两个等边三角形ABE和ADF，连结ED与FC交于点M．
（i）求证：ED=FC．
（ii）若∠ADE=20°，求∠DMC的度数．

【题目】如图，图1是由5个完全相同的正方体搭成的几何体，现将标有E的正方体平移至图2所示的位置，下列说法中正确的是（ ）
①左、右两个几何体的主视图相同
②左、右两个几何体的俯视图相同
③左、右两个几何体的左视图相同．

A.①②③
B.②③
C.①②
D.①③

【题目】如图1，在边长为5的菱形ABCD中，cos∠BAD= ，点E是射线AB上的点，作EF⊥AB，交AC于点F．
（1）求菱形ABCD的面积；
（2）求证：AE=2EF；
（3）如图2，过点F，E，B作⊙O，连结DF，若⊙O与△CDF的边所在直线相切，求所有满足条件的AE的长度．

【题目】（1）已知a+b=5，ab=-2，求代数式（6a-3b-2ab）-（a-8b-ab）的值；

（2）已知2x-y-4=0，求9x27y÷81y的值．

【答案】（1）27；（2）81.

【解析】

（1）运用整式的加减运算顺序先去括号，再合并同类项，根据乘法的分配律将5a+5b变形为5（a+b），最后代入求值即可；

（2）根据幂的乘方，可得同底数幂的乘法，根据同底数幂的乘法，可得答案．

（1）原式=6a-3b-2ab-a+8b+ab=5a+5b-ab=5（a+b）-ab，

当a+b=5，ab=-2时，

原式=5×5-（-2）=27；

（2）9x27y÷81y=32x33y÷34y=32x-y，

由2x-y-4=0，得2x-y=4，

故原式=34=81.

【点睛】

本题考查了幂的乘方，同底数幂的乘法，整式的混合运算和求值的应用，用了整体代入思想．

【题型】解答题
【结束】
23

(1)图中有_____块小正方体；

(2)请在下面方格纸中分别画出它的主视图、左视图和俯视图；

(3)用小正方体搭一几何体，使得它的俯视图和左视图与你在图方格中所画的图一致，若这样的几何体最少要m个小正方体，最多要n个小正方体，则m+n的值为____．