
科目: 来源: 题型:
【题目】如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移,每次平移1个单位,若第1次平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为(用含n的代数式表示)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,点E、F分别在BC、CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在EB′与AD的交点C′处.则BC:AB的值为 . 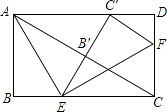
查看答案和解析>>
科目: 来源: 题型:
【题目】小明的父母出去散步,从家走了20分钟到一个离家900米的报亭,母亲随即按原速度返回家,父亲在报亭看了10分钟报纸后,用15分钟返回家,则表示父亲、母亲离家距离与时间之间的关系是(只需填序号). 
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直角三角形纸片ABC中,AB=3,AC=4,D为斜边BC中点,第1次将纸片折叠,使点A与点D重合,折痕与AD交于点P1;设P1D的中点为D1 , 第2次将纸片折叠,使点A与点D1重合,折痕与AD交于点P2;设P2D1的中点为D2 , 第3次将纸片折叠,使点A与点D2重合,折痕与AD交于点P3;…;设Pn﹣1Dn﹣2的中点为Dn﹣1 , 第n次将纸片折叠,使点A与点Dn﹣1重合,折痕与AD交于点Pn(n>2),则AP6的长为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,扇形DOE的半径为3,边长为 ![]() 的菱形OABC的顶点A,C,B分别在OD,OE,
的菱形OABC的顶点A,C,B分别在OD,OE, ![]() 上,若把扇形DOE围成一个圆锥,则此圆锥的高为( )
上,若把扇形DOE围成一个圆锥,则此圆锥的高为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AD为⊙O的直径,作⊙O的内接正三角形ABC,甲、乙两人的作法分别是: 甲:①、作OD的中垂线,交⊙O于B,C两点,
②、连接AB,AC,△ABC即为所求的三角形
乙:①、以D为圆心,OD长为半径作圆弧,交⊙O于B,C两点.
②、连接AB,BC,CA.△ABC即为所求的三角形.
对于甲、乙两人的作法,可判断( )
A.甲、乙均正确
B.甲、乙均错误
C.甲正确、乙错误
D.甲错误,乙正确
查看答案和解析>>
科目: 来源: 题型:
【题目】在如图所示的平面直角坐标系内,画在透明胶片上的ABCD,点A的坐标是(0,2).现将这张胶片平移,使点A落在点A′(5,﹣1)处,则此平移可以是( )
A.先向右平移5个单位,再向下平移1个单位
B.先向右平移5个单位,再向下平移3个单位
C.先向右平移4个单位,再向下平移1个单位
D.先向右平移4个单位,再向下平移3个单位
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:P、Q分别是两条线段a和b上任意一点,线段PQ的长度的最小值叫做线段a与线段b的距离. 已知O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角坐标系中四点.
(1)根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离是;当m=5,n=2时,如图2,线段BC与线段OA的距离为;
(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.
(3)当m的值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M, ①求出点M随线段BC运动所围成的封闭图形的周长;
②点D的坐标为(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m的值使以A、M、H为顶点的三角形与△AOD相似?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某汽车在刹车后行驶的距离s(单位:米)与时间t(单位:秒)之间的关系得部分数据如下表:
时间t(秒) | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | … |
行驶距离s(米) | 0 | 2.8 | 5.2 | 7.2 | 8.8 | 10 | 10.8 | … |
假设这种变化规律一直延续到汽车停止.
(1)根据这些数据在给出的坐标系中画出相应的点;
(2)选择适当的函数表示s与t之间的关系,求出相应的函数解析式;
(3)①刹车后汽车行驶了多长距离才停止? ②当t分别为t1 , t2(t1<t2)时,对应s的值分别为s1 , s2 , 请比较 ![]() 与
与 ![]() 的大小,并解释比较结果的实际意义.
的大小,并解释比较结果的实际意义.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图1,△ABC中,BA=BC,D是平面内不与A、B、C重合的任意一点,∠ABC=∠DBE,BD=BE. 
(1)求证:△ABD≌△CBE;
(2)如图2,当点D是△ABC的外接圆圆心时,请判断四边形BDCE的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com