
科目: 来源: 题型:
【题目】规定两正数a、b之间的一种运算,记作:(a,b),如果![]() ,那么(a,b)=c例如
,那么(a,b)=c例如![]() ,所以(2,8)=3
,所以(2,8)=3
(1)填空:(3,27)=_____,![]() =_____;
=_____;
(2)小明在研究这种运算时发现一个现象:![]() 小明给出了如下的证明:
小明给出了如下的证明:
设![]() ,则
,则![]() ,即
,即![]() .
.
所以![]() ,即(3,4)=x,所以(3n,4n)
,即(3,4)=x,所以(3n,4n)![]() 请你尝试运用这种方法说明下面这个等式成立:
请你尝试运用这种方法说明下面这个等式成立:![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C直角顶点X在△ABC内部,若∠A=30,则∠ABC+∠ACB=_____,∠XBC+∠XCB=________
(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C,直角顶点X还在△ABC内部,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
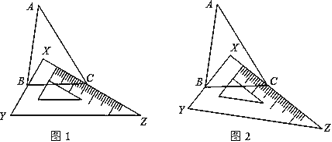
查看答案和解析>>
科目: 来源: 题型:
【题目】钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M,N为该岛的东西两端点)最近距离为14.4km(即MC=14.4km).在A点测得岛屿的西端点M在点A的北偏东42°方向;航行4km后到达B点,测得岛屿的东端点N在点B的北偏东56°方向,(其中N,M,C在同一条直线上),求钓鱼岛东西两端点MN之间的距离(结果精确到0.1km).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,sin56°≈0.83,cos56°≈0.56,tan56°≈1.48)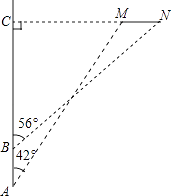
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,在矩形ABCD中,AB=10cm,BC=8cm,点P从A出发,沿A→B→C→D路线运动,到D停止,点P的速度为每秒1cm,a秒时点P改变速度,变为每秒bcm,图②是点P出发x秒后△APD的面积S(cm2)与x(秒)的关系图象,
(1)参照图②,求a、b及图②中的c值;
(2)设点P离开点A的路程为y(cm),请写出动点P改变速度后y与出发后的运动时间x(秒)的关系式,并求出点P到达DC中点时x的值.
(3)当点P出发多少秒后,△APD的面积是矩形ABCD面积的![]() .
.
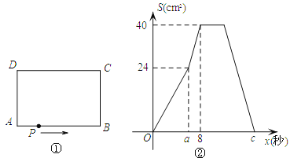
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,将矩形ABCD沿DE折叠,使顶点A落在DC上的点A′处,然后将矩形展平,沿EF折叠,使顶点A落在折痕DE上的点G处.再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处.如图2.

(1)求证:EG=CH;
(2)已知AF=![]() ,求AD和AB的长.
,求AD和AB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图(1)、图(2).在图(1)中,∠B=90°,∠A=30°;图(2)中,∠D=90°,∠F=45°.图(3)是该同学所做的一个实验:他将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上,移动开始时,点D与点A重合.
(1)△DEF在移动过程中,∠FCE与∠CFE度数之和是否为定值,请加以说明;
(2)能否将△DEF移动至某位置,使F、C的连线与AB平行?若能,求出∠CFE的度数;若不能,请说明理由.
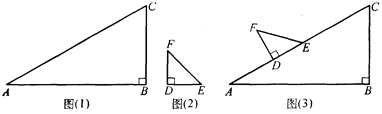
查看答案和解析>>
科目: 来源: 题型:
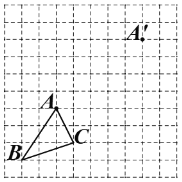
【题目】如图,在边长为1个单位长度的小正方形组成的网格中.
(1)把△ABC平移至![]() 的位置,使点A与
的位置,使点A与![]() 对应,得到△
对应,得到△![]() ;
;
(2)图中可用字母表示,与线段![]() 平行且相等的线有:________;
平行且相等的线有:________;
(3)求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】点P(x ,y)在第一象限,且x+y=8 ,点A的坐标为(6,0).设三角形OPA的面积为S .
(1)用含x的解析式表示S ,写出 x的取值范围.
(2)当点P的横坐标为5的时候,三角形OPA的面积是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,∠BAE +∠AED=180°,∠1=∠2,那么∠M=∠N.下面是推理过程,请你完成.
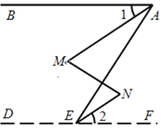
解:∵∠BAE+∠AED=180°(已知)
∴AB∥DE(______).
∴∠BAE=∠AEF(______).
又∵∠1=∠2(已知)
∴ ∠BAE∠1=∠AEF_____(等式性质),即 ∠MAE = ∠NEA .
∴_______∥______(______).
∴∠M=∠N(两直线平行,内错角相等).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com