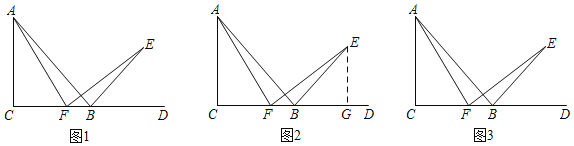
已知：如图1，在Rt△ABC中，∠C=90°，AC=BC，延长CB到点D，∠DBE=45°，点F是边BC上一点，连结AF，作FE⊥AF，交BE于点E．

（1）求证：∠CAF=∠DFE；

（2）求证：AF=EF．

经过独立思考后，老师让同学们小组交流．小辉同学说出了对于第二问的想法：“我想通过构造含有边AF和EF的全等三角形，因此我过点E作EG⊥CD于G（如图2所示），如果能证明Rt△ACF和Rt△FGE全等，问题就解决了．但是这两个三角形证不出来相等的边，好像这样作辅助线行不通．”小亮同学说：“既然这样作辅助线证不出来，再考虑有没有其他添加辅助线的方法．”请你顺着小亮同学的思路在图3中继续尝试，并完成（1）、（2）问的证明．

【题目】关于x的一元二次方程x2﹣3x﹣k=0有两个不相等的实数根．
（1）求k的取值范围；
（2）若这个方程有一个根为﹣2，求k的值和方程的另一个根．

（1）求2⊕（﹣1）的值；

（2）求﹣3⊕（﹣4⊕）的值；

（3）试用学习有理数的经验和方法来探究这种新运算“⊕”是否具有交换律？请写出你的探究过程．

【题目】2017年8月1日是中国人民解放军成立90周年纪念日，某学校团委为此准备举行“学唱红歌”歌咏比赛，要确定一首喜欢人数最多的歌曲为每班必唱曲目，为此提供代号为A，B，C，D四首备选曲目让学生选择，经过抽样调查，并将采集的数据绘制如下两幅不完整的统计图．请根据图①、图②所提供的信息，解答下列问题：
（1）本次抽样调查的学生有名，其中选择曲目代号为A的学生所对应圆心角的度数为；
（2）请将图②补充完整；
（3）若该校共有1800名学生，根据抽样调查的结果估计全校共有多少名学生选择代号为C的曲目为必唱歌曲？

【题目】如图，点A、F、C、D在同一直线上，AB∥DE，AC=DF，AB=DE．
（1）求证：四边形BCEF是平行四边形；
（2）若∠ABC=90°，AB=8，BC=6，当AF为何值时，四边形BCEF是菱形．

（1）若以小明家为原点，向东为正方向，用1个单位长度表示1千米，请将超市、爷爷家和姥爷家的位置在下面数轴上分别用点A、B、C表示出来；

（2）超市和姥爷家相距多少千米？

（3）若小轿车每千米耗油0.08升，求小明一家从出发到返回家，小轿车的耗油量．

【题目】先化简（ ﹣ ）÷ ，然后从不等式组 的解集中选取一个你喜欢的x的值代入求值．

【题目】矩形纸片ABCD中，AB=5，AC=3，将纸片折叠，使点B落在边CD上的B′处，折痕为AE．在折痕AE上存在一点P到边CD的距离与到点B的距离相等，则此相等距离为 ．

①确定所有可能发生的结果个数和其中出现所求事件的结果个数

②计算所求事件发生的可能性大小，即 (所求事件)

③列出所有可能发生的结果，并判断每个结果发生的可能性都相等

【题目】随着北京申办冬奥会的成功，愈来愈多的同学开始关注我国的冰雪体育项目. 小健从新闻中了解到：在2018年平昌冬奥会的短道速滑男子500米决赛中，中国选手武大靖以39秒584的成绩打破世界纪录，收获中国男子短道速滑队在冬奥会上的首枚金牌. 同年11月12日，武大靖又以39秒505的成绩再破世界纪录. 于是小健对同学们说：“2022年北京冬奥会上武大靖再获金牌的可能性大小是.”你认为小健的说法_________（填“合理”或“不合理”），理由是__________________________.