
科目: 来源: 题型:
【题目】综合与探究
问题背景
在综合实践课上,老师让同学们根据如下问题情境,写出两个教学结论:
如图,点C在线段BD上,点E在线段AC上.∠ACB=∠ACD=90°,AC=BC;DC=CE,M,N分别是线段BE,AD上的点.
“兴趣小组”写出的两个教学结论是:①△BCE≌△ACD;②当CM,CN分别是△BCE和△ACD的中线时,△MCN是等腰直角三角形.
解决问题
(1)请你结合图(1).证明“兴趣小组”所写的两个结论的正确性.
类比探究
受到“兴趣小组”的启发,“实践小组”的同学们写出如下结论:如图(2),当∠BCM=∠ACN时,△MCN是等腰直角三角形.
(2)“实践小组”所写的结论是否正确?请说明理由.
感悟发现
“奋进小组”认为:当点M,N分别是BE,AD的三等分点时,△MCN仍然是等腰直角三角形请你思考:
(3)“奋进小组”所提结论是否正确?答: (填“正确”、“不正确”或“不一定正确”.)
(4)反思上面的探究过程,请你添加适当的条作,再写出使得△MCN是等腰直角三角形的数学结论.(所写结论必须正确,写出1个即可,不要求证明)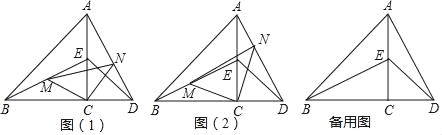
查看答案和解析>>
科目: 来源: 题型:
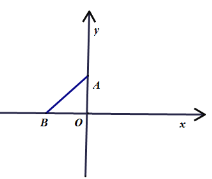
【题目】如图,在直角坐标平面内有两点![]() 、
、![]() ,且
,且![]() 、
、![]() 两点之间的距离等于
两点之间的距离等于![]() (
(![]() 为大于0的已知数),在不计算
为大于0的已知数),在不计算![]() 的数值条件下,完成下列两题:
的数值条件下,完成下列两题:
(1)以学过的知识用一句话说出![]() 的理由;
的理由;
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 是等腰三角形,如果存在,请写出点
是等腰三角形,如果存在,请写出点![]() 的坐标,并求
的坐标,并求![]() 的面积;如果不存在,请说明理由.
的面积;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目: 来源: 题型:
【题目】结合“爱市西,爱生活,会创新”的主题,某同学设计了一款“地面霓虹探测灯”,增加美观的同时也为行人的夜间行路带去了方便.他的构想如下:在平面内,如图1所示,灯![]() 射线从
射线从![]() 开始顺时针旋转至
开始顺时针旋转至![]() 便立即回转,灯
便立即回转,灯![]() 射线从
射线从![]() 开始顺时针旋转至
开始顺时针旋转至![]() 便立即回转,两灯不停交叉照射巡视.若灯
便立即回转,两灯不停交叉照射巡视.若灯![]() 转动的速度是每秒2度,灯
转动的速度是每秒2度,灯![]() 转动的速度是每秒1度.假定主道路是平行的,即
转动的速度是每秒1度.假定主道路是平行的,即![]() ,且
,且![]() .
.
(1)填空:![]() ______
______![]() ;
;
(2)若灯![]() 射线先转动60秒,灯
射线先转动60秒,灯![]() 射线才开始转动,在灯
射线才开始转动,在灯![]() 射线到达
射线到达![]() 之前,
之前,![]() 灯转动几秒,两灯的光束互相平行?
灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯![]() 射线到达
射线到达![]() 之前,若射出的光束交于点
之前,若射出的光束交于点![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,则在转动过程中,请探究
,则在转动过程中,请探究![]() 与
与![]() 的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
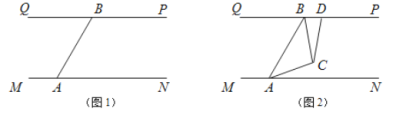
查看答案和解析>>
科目: 来源: 题型:
【题目】随着科技与经济的发展,机器人自动化线的市场越来越大,并且逐渐成为自动化生产线的主要方式某化工厂要在规定时间内搬运1800千克化工原料,现有A,B两种机器人可供选择,已知A型机器人每小时完成的工作量是B型机器人的1.5倍,A型机器人单独完成所需的时间比B型机器人少10小时.
(1)求两种机器人每小时分别搬运多少千克化工原料?
(2)若A型机器人工作1小时所需的费用为80元,B型机器人工作1小时所需的费用为60元,若该工厂在两种机器人中选择其中的一种机器人单独完成搬运任务,则选择哪种机器人所需费用较小?请计算说明.
查看答案和解析>>
科目: 来源: 题型:
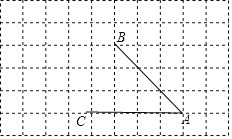
【题目】如图,由相同边长的小正方形组成的网格图形,A、B、C都在格点上,利用网格画图:(注:所画线条用黑色签字笔描黑)
(1)过点C画AB的平行线;
(2)过点B画AC的垂线,垂足为点G;过点B画AB的垂线,交AC的延长线于H.
(3)点B到AC的距离是线段 的长度,线段AB的长度是点 到直线 的距离.
(4)线段BG、AB的大小关系为:BG AB(填“>”、“<”或“=”),理由是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料,解决提出的问题:
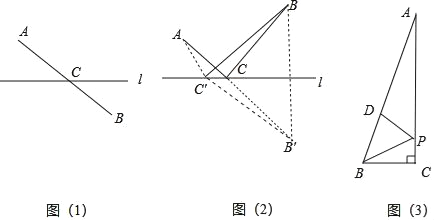
最短路径问题:如图(1),点A,B分别是直线l异侧的两个点,如何在直线l上找到一个点C,使得点C到点A,点B的距离和最短?我们只需连接AB,与直线l相交于一点,可知这个交点即为所求.
如图(2),如果点A,B分别是直线l同侧的两个点,如何在l上找到一个点C,使得这个点到点A、点B的距离和最短?我们可以利用轴对称的性质,作出点B关于的对称点B,这时对于直线l上的任一点C,都保持CB=CB,从而把问题(2)变为问题(1).因此,线段AB与直线l的交点C的位置即为所求.
为了说明点C的位置即为所求,我们不妨在直线上另外任取一点C′,连接AC′,BC′,B′C′.因为AB′≤AC′+C′B′,∴AC+CB<AC'+C′B,即AC+BC最小.
任务:
数学思考
(1)材料中划线部分的依据是 .
(2)材料中解决图(2)所示问题体现的数学思想是 .(填字母代号即可)
A.转化思想
B.分类讨论思想
C.整体思想
迁移应用
(3)如图,在Rt△ABC中,∠C=90°,∠BAC=15°,点P为C边上的动点,点D为AB边上的动点,若AB=8cm,则BP+DP的最小值为 cm.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点E,点F分别在菱形ABCD的边AB,AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若 ![]() =2,则
=2,则 ![]() 的值为( )
的值为( )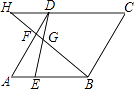
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为O.以点C为圆心,BC为半径作弧AB,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com