
科目: 来源: 题型:
【题目】“小组合作学习”成为我区推动课堂教学改革,打造自主高效课堂的重要举措.某中学从全校学生中随机抽取100人作为样本,对“小组合作学习”实施前后学生的学习兴趣变化情况进行调查分析,统计如下: 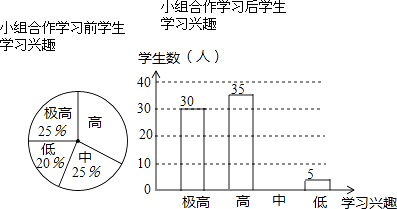
请结合图中信息解答下列问题:
(1)小组合作学习前学生学习兴趣为“高”的所占的百分比为;
(2)补全小组合作学习后学生学习兴趣的统计图;
(3)通过“小组合作学习”前后学生学习兴趣的对比,请你估计全校2000名学生中学习兴趣获得提高的学生有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,A、B两点分别在x轴和y轴上,OA=1,OB= ![]() ,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1 , 连接A1B1 , 再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 .
,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1 , 连接A1B1 , 再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 . 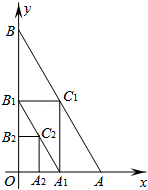
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为 . 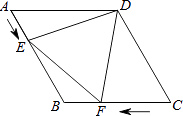
查看答案和解析>>
科目: 来源: 题型:
【题目】(8分)如图,在ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.

(1)求证:AE=AF;
(2)求∠EAF的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(﹣6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第18次翻转后点C的纵坐标是_____.
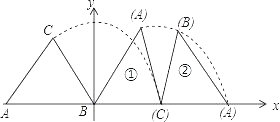
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,E,F分别是ABCD的边AD,BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折得到EFC′D′,ED′交BC于点C,则△GEF的周长为_____.
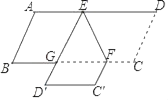
查看答案和解析>>
科目: 来源: 题型:
【题目】已知△ABC,点D、F分别为线段AC、AB上两点,连接BD、CF交于点E.
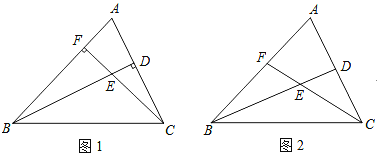
(1)若BD⊥AC,CF⊥AB,若BE=4,CE=2,求CD:BF;
(2)若BD平分∠ABC,CF平分∠ACB,如图2所示,猜想∠BEC与∠A的数量关系;并说明理由.
(3)在(2)的条件下,若∠A=60°,试说明:BC=BF+CD.
查看答案和解析>>
科目: 来源: 题型:
【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:![]()
![]()
![]()
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为![]() 和
和![]() (其中
(其中![]() 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
(3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,求证:∠ACD=∠B;
(2)如图②,在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,判断△ADE的形状?并说明理由?
(3)如图③,在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,点C,B,E在同一直线上,若AB⊥BD,AB=BD,则CE与AC,DE有什么等量关系,并证明.

查看答案和解析>>
科目: 来源: 题型:
【题目】(1)已知2x﹣y=8,求代数式[x2+y2﹣(x﹣y)2+2y(x﹣y)]÷4y的值.
(2)阅读下列材料:常用分解因式的方法有提取公因式法、公式法,但有部分多项式只单纯用上述方法就无法分解,如x2﹣2xy+y2﹣16,我们细心观察这个式子就会发现,前三项符合完全平方公式,进行变形后可以与第四项结合再运用平方差公式进行分解.过程如下:x2﹣2xy+y2﹣16=(x﹣y)2﹣16=(x﹣y+4)(x﹣y﹣4)这种分解因式的方法叫分组分解法.利用这种分组的思想方法解决下列问题:
已知a,b,c分别是△ABC三边的长,且2a2+b2+c2﹣2a(b+c)=0请判断△ABC的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com