
科目: 来源: 题型:
【题目】随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):
选项 | 频数 | 频率 |
A | 10 | m |
B | n | 0.2 |
C | 5 | 0.1 |
D | p | 0.4 |
E | 5 | 0.1 |
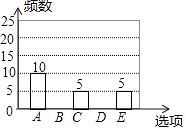
根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图.
(3)若该中学约有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调查结果,就中学生如何合理使用手机给出你的一条建议.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)已知一个角的补角比它的余角的 3 倍大 30°,求这个角的度数;
(2)如图,点 C、D在线段 AB上, D是线段 AB的中点, AC ![]() AD , AB6,求线段 CD的长.
AD , AB6,求线段 CD的长.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB∶OE=3∶2.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB 的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.当一个点停止运动时时,另一个点也随之停止运动.设运动时间为t.
(1)用含有t的代数式表示CP.
(2)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,∠BAC=90°,AD⊥BC,垂足为点 D.下列说法中:①∠B的余角只有∠BAD;②∠B=∠C;③线段 AB 的长度表示点 B 到直线 AC 的距离;④AB·AC=BC·AD;一定正确的有( )
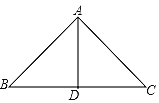
A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目: 来源: 题型:
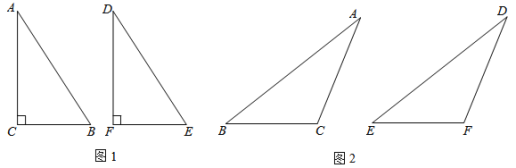
【题目】学习全等三角形的判定方法以后,我们知道“已知两边和一角分别相等的两个三角形不一定全等”,但下列两种情形还是成立的.
(1)第一情形(如图1)在△ABC和△DEF中,∠C=∠F=90°,AC=DF,AB=DE,则根据__________,得出△ABC≌△DEF;
(2)第二情形(如图2)在△ABC和△DEF中,∠C=∠F(∠C和∠F均为钝角),AC=DF,AB=DE,求证:△ABC≌△DEF.
查看答案和解析>>
科目: 来源: 题型:
【题目】某景区修建一栋复古建筑,其窗户设计如图所示.圆O的圆心与矩形ABCD对角线的交点重合,且圆与矩形上下两边相切(E为上切点),与左右两边相交(F,G为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m,根据设计要求,若∠EOF=45°,则此窗户的透光率(透光区域与矩形窗面的面积的比值)为 . 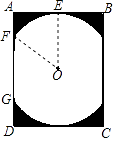
查看答案和解析>>
科目: 来源: 题型:
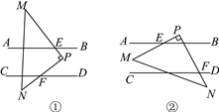
【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F.
(1)当△PMN所放位置如图①所示时,求出∠PFD与∠AEM的数量关系;
(2)当△PMN所放位置如图②所示时,求证:∠PFD-∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=15°,∠PEB=30°,求∠N的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】观察下列图形,它是把一个三角形分别连接这个三角形三边的中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,…将这种做法继续下去(如图2,图3…),则图6中挖去三角形的个数为( ) 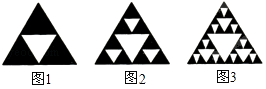
A.121
B.362
C.364
D.729
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com