
科目: 来源: 题型:
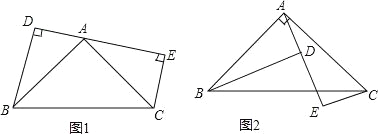
【题目】已知:如图1,△ABC是等腰直角三角形,∠BAC=90°,DE是经过点A的直线,作BD⊥DE,CE⊥DE,
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,我们能得到什么结论?并证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,A点坐标为(2,4),B点坐标为(﹣3,﹣2),C点坐标为(3,1).
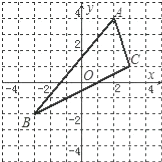
(1)在图中画出△ABC关于y轴对称的△A′B′C′(不写画法),并写出点A′,B′,C′的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
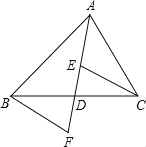
【题目】如图,在△ABC中,点D是BC的中点,连接AD,E,F分别是AD和AD延长线上的点.且DE=DF,连接BF,CE,下列说法中:①△ABD和△ACD的面积相等;②∠BAD=∠CAD;③BF∥CE;④CE=BF,其中,正确的说法有__________(填序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,A(a,b)、B(1,4)(a>1)是反比例函数y= ![]() (x>0)图象上两点,过A、B分别作x轴、y轴的垂线,垂足分别为C、D、E、F,AE、BD交于点G.则四边形ACDG的面积随着a的增大而 . (填“减小”、“不变”或“增大”)
(x>0)图象上两点,过A、B分别作x轴、y轴的垂线,垂足分别为C、D、E、F,AE、BD交于点G.则四边形ACDG的面积随着a的增大而 . (填“减小”、“不变”或“增大”) 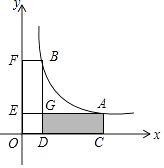
查看答案和解析>>
科目: 来源: 题型:
【题目】我们来定义一种新运算:对于任意实数x、y,“※”为a※b=(a+1)(b+1)﹣1
(1)计算(﹣3)※9
(2)嘉琪研究运算“※”之后认为它满足交换律,你认为她的判断 (正确、错误)
(3)请你帮助嘉琪完成她对运算“※”是否满足结合律的证明.
证明:由已知把原式化简得a※b=(a+1)(b+1)﹣1=ab+a+b
∵(a※b)※c=(ab+a+b)※c=
a※(b※c)=
∴
∴运算“※”满足结合律.

查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为________________________________.

查看答案和解析>>
科目: 来源: 题型:
【题目】快、慢两车分别从相距180 km的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早![]() h,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(km)与所用时间x(h)的函数图象如图所示,请结合图象信息解答下列问题:
h,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(km)与所用时间x(h)的函数图象如图所示,请结合图象信息解答下列问题:
(1)请直接写出快、慢两车的速度;
(2)求快车返回过程中y(km)与x(h)的函数关系式;
(3)两车出发后经过多长时间相距90 km的路程?直接写出答案.

查看答案和解析>>
科目: 来源: 题型:
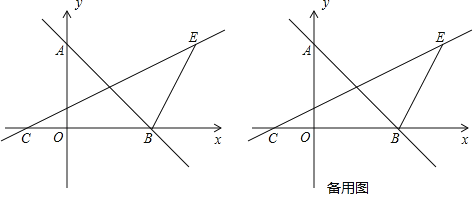
【题目】如图,一次函数y=﹣x+4的图象与y轴交于点A,与x轴交于点B,过AB中点D的直线CD交x轴于点C,且经过第一象限的点E(6,4).
(1)求A,B两点的坐标及直线CD的函数表达式;
(2)连接BE,求△DBE的面积;
(3)连接DO,在坐标平面内找一点F,使得以点C,O,F为顶点的三角形与△COD全等,请直接写出点F的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() ﹣1来表示
﹣1来表示![]() 的小数部分,事实上,小明的表示方法是有道理的,因为
的小数部分,事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是
的整数部分是1,将这个数减去其整数部分,差就是![]() 的小数部分,又例如:∵22<(
的小数部分,又例如:∵22<(![]() )2<32,即2<
)2<32,即2<![]() <3,∴
<3,∴![]() 的整数部分为2,小数部分为(
的整数部分为2,小数部分为(![]() ﹣2).
﹣2).
请解答:
(1)![]() 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .
(2)如果![]() 的小数部分为a,
的小数部分为a,![]() 的整数部分为b,求a+b﹣
的整数部分为b,求a+b﹣![]() 的值.
的值.
(3)已知x是3+![]() 的整数部分,y是其小数部分,直接写出x﹣y的值.
的整数部分,y是其小数部分,直接写出x﹣y的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com