
科目: 来源: 题型:
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,即确定一个月销售目标,根据目标完成的情况对营业员进行适当的奖惩.为了确定一个适当的目标,商场统计了每个营业员在某月的销售额,统计图如下:
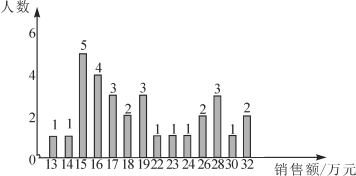
请你结合统计图和平均数、众数和中位数解答下列问题:(结果保留整数)
(1)月销售额在哪个值的人最多?月销售额处于中间的是多少?月平均销售额是多少?
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知点![]() 分别在线段
分别在线段![]() 上,
上,![]() 交
交![]() 于点
于点![]() 平分
平分![]() .
.
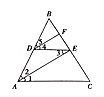
(1)求证:![]() 平分
平分![]() 阅读下列推理过程,并将推理过程补充完整.
阅读下列推理过程,并将推理过程补充完整.
证明:![]() 平分
平分![]() ,(已知)
,(已知)
![]() (角平分线的定义)
(角平分线的定义)
![]() ,(已知)
,(已知)
![]() ( )
( )
故 .(等量代换)
![]() ,(已知)
,(已知)
![]() ,( )
,( )
![]() ,( )
,( )
![]() ,
,
![]() 平分
平分![]() .( )
.( )
(2)若![]() ,请直接写出图中所有与
,请直接写出图中所有与![]() 互余的角.
互余的角.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是( )
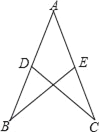
A. AB=AC B. ∠B=∠C
C. BE=CD D. ∠ADC=∠AEB
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,小强从A处出发沿北偏东70°方向行走,走至B处,又沿着北偏西30°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是( )
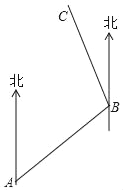
A. 左转 80° B. 右转80° C. 右转 100° D. 左转 100°
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C. 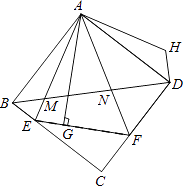
(1)求证:四边形ABCD是正方形;
(2)连接BD分别交AE、AF于点M、N,将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH,试判断线段MN、ND、DH之间的数量关系,并说明理由.
(3)若EG=4,GF=6,BM=3 ![]() ,求AG、MN的长.
,求AG、MN的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在长方形纸片ABCD中,AB=m,AD=n,将两张边长分别为6和4的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.
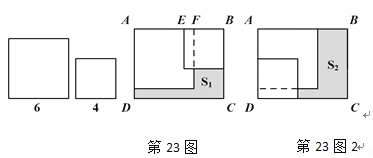
(1)在图1中,EF= ,BF= ;(用含m的式子表示)
(2)请用含m、n的式子表示图1,图2中的s1,s2,若m-n=2,请问S2-S1的值为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c的顶点为M(﹣2,﹣4),与x轴交于A、B两点,且A(﹣6,0),与y轴交于点C.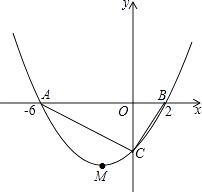
(1)求抛物线的函数解析式;
(2)求△ABC的面积;
(3)能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大?若能,请求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】微信运动和腾讯公益推出了一个爱心公益活动:一天中走路步数达到10000步及以上可通过微信运动和腾讯基金会向公益活动捐款,如果步数在10000步及以上,每步可捐0.0002元;若步数在10000步以下,则不能参与捐款.
(1)老赵某天的步数为13000步,则他当日可捐多少钱?
(2)已知甲、乙、丙三人某天通过步数共捐了8.4元,且甲的步数=乙的步数=丙步数的3倍,则丙走了多少步?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com