
科目: 来源: 题型:
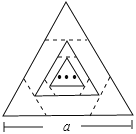
【题目】边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于![]() 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用实线条画出对称轴。

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,BA=BC,BD是三角形的角平分线,DE∥BC交AB于E,下列结论:①∠1=∠3;②DE= ![]() AB;③S△ADE=
AB;③S△ADE= ![]() S△ABC . 正确的有( )
S△ABC . 正确的有( )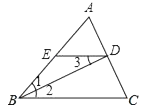
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目: 来源: 题型:
【题目】为庆祝“六一”儿童节,某市中小学统一组织文艺汇演,甲、乙两所学校共92人(其中甲校的人数多于乙校的人数,且甲校的人数不足90人)准备统一购买服装参加演出;下面是某服装厂给出的演出服装的价格表
购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
(1)如果两所学校分别单独购买服装一共应付5000元,甲、乙两所学校各有多少学生准备参加演出?
(2)如果甲校有10名同学抽调去参加书法绘画比赛不能参加演出,请你为两所学校设计一种最省钱的购买服装方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】有两种包装盒,大盒比小盒可多装20克某一物品.已知120克这一物品单独装满小盒比单独装满大盒多1盒.
(1)问小盒每个可装这一物品多少克?
(2)现有装满这一物品两种盒子共50个.设小盒有n个,所有盒子所装物品的总量为w克. ①求w关于n的函数解析式,并写出定义域;
②如果小盒所装物品总量与大盒所装物品总量相同,求所有盒子所装物品的总量.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读理解:
我们知道:一条线段有两个端点,线段![]() 和线段
和线段![]() 表示同一条线段. 若在直线
表示同一条线段. 若在直线![]() 上取了三个不同的点,则以它们为端点的线段共有 条;若取了四个不同的点,则共有线段 条;…;依此类推,取了
上取了三个不同的点,则以它们为端点的线段共有 条;若取了四个不同的点,则共有线段 条;…;依此类推,取了![]() 个不同的点,共有线段条.(用含
个不同的点,共有线段条.(用含![]() 的代数式表示)
的代数式表示)
类比探究:
以一个锐角的顶点为端点向这个角的内部引射线.
(1)若引出两条射线,则所得图形中共有 个锐角;
(2)若引出![]() 条射线,则所得图形中共有 个锐角.(用含
条射线,则所得图形中共有 个锐角.(用含![]() 的代数式表示)
的代数式表示)
拓展应用:
一条铁路上共有8个火车站,若一列火车往返过程中必须停靠每个车站,则铁路局需为这条线路准备多少种车票?
查看答案和解析>>
科目: 来源: 题型:
【题目】一辆货车从超市出发,向东走了3千米到达A地,继续向东走25千米到达B地,然后向西走了10千米到达C地,最后回到超市。
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,画出数轴并在数轴上表示出A地、B地、C地的位置;
(2)求C地距离A地多远?
(3)货车一共行驶了多少千米?
(4)货车每千米耗油0.5升,这次共耗油多少升?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC和△A'B'C'关于直线m对称.
(1)结合图形指出对称点;
(2)若连接AA',直线m与线段AA'有什么关系?
(3)BC与B'C'的交点,AB与A'B'的交点分别与直线m有怎样的关系?若延长AC与A'C',其交点与直线m有怎样的关系?你发现了什么规律?

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在Rt△ABC和Rt△BCD中,∠ABC=∠BCD=90°,BD与AC相交于点E,AB=9,cos∠BAC= ![]() ,tan∠DBC=
,tan∠DBC= ![]() .
. 
求:
(1)边CD的长;
(2)△BCE的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】点C为直线AB上一点,点M、N分别是线段AC、线段BC的中点。
(1)如图,若C为线段AB上一点,AC=6,BC=4,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+BC=![]() 其他条件不变,请直接写出线段MN的长(用含
其他条件不变,请直接写出线段MN的长(用含![]() 的代数式表示);
的代数式表示);
(3)若C为线段AB的延长线上一点,且满足AC-BC=![]() 其他条件不变,请直接写出线段MN的长(用含
其他条件不变,请直接写出线段MN的长(用含![]() 的代数式表示)。
的代数式表示)。
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com