
科目: 来源: 题型:
【题目】平面上,矩形ABCD与直径为QP的半圆K如图1摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转,设旋转角为α(0°≤α≤60°).
发现:如图2,当点P恰好落在BC边上时,求a的值即阴影部分的面积;
拓展:如图3,当线段OQ与CB边交于点M,与BA边交于点N时,设BM=x(x>0),用含x的代数式表示BN的长,并求x的取值范围.
探究:当半圆K与矩形ABCD的边相切时,直接写出sinα的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直角坐标系中,Rt△AOB的两条直角边OA,OB分别在x轴的负半轴,y轴的负半轴上,且OA=2,OB=1.将Rt△AOB绕点O按顺时针方向旋转90°,再把所得的像沿x轴正方向平移1个单位,得△CDO.

(1)写出点A,B,C,D的坐标;
(2)求点A和点C之间的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两家蓝莓采摘园的草莓品质相同,销售价格都是每千克30元,“五一”假期,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园购买60元的门票,采摘的蓝莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘的蓝莓超过10千克后,超过部分五折优惠,优惠期间,设某游客的蓝莓采摘量为![]() (千克),在甲采摘园所需总费用为
(千克),在甲采摘园所需总费用为![]() (元),在乙采摘园所需总费用为
(元),在乙采摘园所需总费用为![]() (元).
(元).
(1)当采摘量超过10千克时,求![]() 与
与![]() 的关系式;
的关系式;
(2)若要采摘40千克蓝莓,去哪家比较合算?请计算说明.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=2.Rt△AB′C′可以看作是由Rt△ABC绕A点逆时针方向旋转60°得到的,求线段 B′C的长.
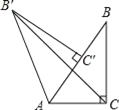
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.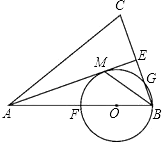
(1)求证:AE与⊙O相切;
(2)当BC=4,AC=6,求⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
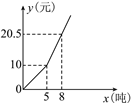
【题目】某市为了节约用水,采用分段收费标准.若某户居民每月应交水费y(元)与用水量x(吨)之间关系的图象如图,根据图象回答:
(1)该市自来水收费时,若使用不足5吨,则每吨收费多少元?超过5吨部分每吨收费多少元?
(2)若某户居民每月用水3.5吨,应交水费多少元?若某月交水费17元,该户居民用水多少吨?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
查看答案和解析>>
科目: 来源: 题型:
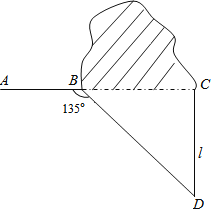
【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(![]() ≈1.414,精确到1米)
≈1.414,精确到1米)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:线段![]() 、
、![]() 、
、![]() ;
;
求作:△ABC,使![]() ,
, ![]() ,
, ![]() ;
;

【答案】答案见解析
【解析】试题分析:先画出与![]() 相等的角,再画出
相等的角,再画出![]() 的长,连接
的长,连接![]() ,则
,则![]() 即为所求三角形.
即为所求三角形.
试题解析:如图所示:①先画射线BC,
②以α的顶点为圆心,任意长为半径画弧,分别交α的两边交于为A′,C′;
③以相同长度为半径,B为圆心,画弧,交BC于点F,以F为圆心,C′A′为半径画弧,交于点E;
④在BF上取点C,使CB=a,以B为圆心,c为半径画圆交BE的延长线于点A,连接AC,
结论:△ABC即为所求三角形.

【题型】解答题
【结束】
15
【题目】已知:线段![]() ,
, ![]() ,求作:
,求作: ![]() ,使
,使![]() ,
, ![]() .
.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.
(1)求抛物线的表达式;
(2)D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交线段AM于点F,求线段DF长度的最大值,并求此时点D的坐标;
(3)抛物线上是否存在一点P,作PN垂直x轴于点N,使得以点P、A、N为顶点的三角形与△MAO相似(不包括全等)?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com