
科目: 来源: 题型:
【题目】如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件,使△ABC ≌ △DEC,则添加的条件不能为( )
A. ∠B=∠E B. AC=DC C. ∠A=∠D D. AB=DE
查看答案和解析>>
科目: 来源: 题型:
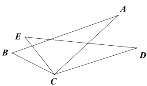
【题目】如图所示,E为正方形ABCD的边BC延长线上一点,且CE=AC,AE交CD于点F,那么∠AFC的度数为( )

A. 112.5° B. 125° C. 135° D. 150°
查看答案和解析>>
科目: 来源: 题型:
【题目】某汽车制造厂开发了一款新式电动汽车,计划一年生产安装240辆。由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人:他们经过培训后上岗,也能独立进行电动汽车的安装。生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车。
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘新工人若干名(新工人人数少于10人)和抽调的熟练工合作,刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
查看答案和解析>>
科目: 来源: 题型:
【题目】问题情境
在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
操作发现
(1)如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;
结论应用
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则∠CFG等于______(用含α的式子表示).

查看答案和解析>>
科目: 来源: 题型:
【题目】将一副三角板中的两块直角三角板的直角顶点C按如图方式叠放在一起,友情提示:∠A=60°,∠D=30°,∠E=∠B=45°.
(1)①若∠DCB=45°,则∠ACB的度数为 .
②若∠ACB=140°,则∠DCE的度数为 .
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<90°且点E在直线AC的上方时,当这两块三角尺有一组边互相平行时,请直接写出∠ACE角度所有可能的值(不必说明理由).

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度数.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB、BC、AC三边的长分别是![]() ,
,![]() ,
,![]() .
.
(1)△ABC的面积是 ;
(2)请在图1中作出△ABC关于直线l对称的△A1B1C1;
(3)请在图2中画出△DEF,是DE、EF、DF三边的长分别是![]() ,
,![]() ,
,![]() ,并判断△DEF的形状,说明理由.
,并判断△DEF的形状,说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】感知:
如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°.判断DB与DC的大小关系并证明.
探究:
如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,DB与DC的大小关系变吗?请说明理由.
应用:
如图③,四边形ABDC中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC= .(用含a的代数式表示)

查看答案和解析>>
科目: 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是( )

A. 4nB. 4mC. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com