
科目: 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,己知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( ) ①△ABC与△DEF是位似图形; ②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比为1:2;④△ABC与△DEF的面积比为4:1.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1.
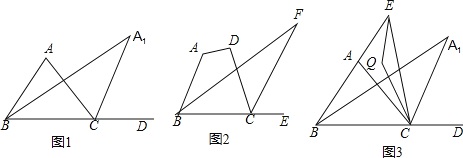
(1)当∠A为70°时,
∵∠ACD -∠ABD=∠____________
∴∠ACD -∠ABD=______________°
∵BA1、CA1是∠ABC的角平分线与∠ACB的外角∠ACD的平分线
∴∠A1CD -∠A1BD=![]() (∠ACD-∠ABD)
(∠ACD-∠ABD)
∴∠A1=___________°;
(2)∠A1BC的角平分线与∠A1CD的角平分线交于A2,∠A2BC与A2CD的平分线交于A3,如此继续下去可得A4、…、An,请写出∠A与∠An 的数量关系____________;
(3)如图2,四边形ABCD中,∠F为∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的角,若∠A+∠D=230度,则∠F= .
(4)如图3,若E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,当E滑动时有下面两个结论:①∠Q+∠A1的值为定值;②∠Q —∠A1的值为定值.
其中有且只有一个是正确的,请写出正确的结论,并求出其值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知等腰Rt△ABC,∠BAC=90°,AB=AC,点D为△ABC内部一点,连接AD、BD、CD,点H为BD中点,连接AH,且∠BAH=∠ACD.
(1)如图1,若∠ADB=90°,求证:∠DAH=45°;
(2)如图2,若∠ADB<90°,(1)问中的结论是否成立,若成立,请证明;若不成立,请说明理由.
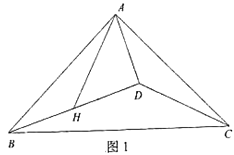
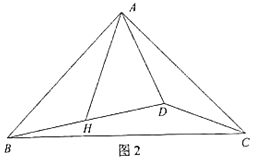
查看答案和解析>>
科目: 来源: 题型:
【题目】有5张边长为2的正方形纸片,4张边长分别为2、3的矩形纸片,6张边长为3的正方形纸片,从其中取出若干张纸片,且每种纸片至少取一张,把取出的这些纸片拼成一个正方形(原纸张进行无空隙、无重叠拼接),则拼成正方形的边长最大为 ( )
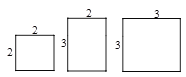
A. 6B. 7C. 8D. 9
查看答案和解析>>
科目: 来源: 题型:
【题目】母亲节前夕,某淘宝店主从厂家购进A、B两种礼盒,已知A、B两种礼盒的单价比为2:3,单价和为200元.
(1)求A、B两种礼盒的单价分别是多少元?
(2)该店主购进这两种礼盒恰好用去9600元,且购进A种礼盒最多36个,B种礼盒的数量不超过A种礼盒数量的2倍,共有几种进货方案?
(3)根据市场行情,销售一个A种礼盒可获利10元,销售一个B种礼盒可获利18元.为奉献爱心,该店主决定每售出一个B种礼盒,为爱心公益基金捐款m元,每个A种礼盒的利润不变,在(2)的条件下,要使礼盒全部售出后所有方案获利相同,m值是多少?此时店主获利多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】随着出行方式的多样化,某地区打车有三种乘车方式,收费标准如下(假设打车的平均车速为30千米/小时):
网约出租车 | 网约顺风车 | 网约专车 |
3千米以内:12元 | 1.5元/千米 | 2元/千米 |
超过3千米的部分:2.4元/千米 | 0.5元/分钟 | 0.6元/分钟 |
(如:乘坐6千米,耗时12分钟,网约出租车的收费为:12+2.4×(6-3)=19.2(元);网约顺风车的收费为:6×1.5+12×0.5=15(元);网约专车的收费为:6×2+12×0.6=19.2(元))
请据此信息解决如下问题:
(1)王老师乘车从纵棹园去汽车站,全程8千米,如果王老师乘坐网约出租车,需要支付的打车费用为______元;
(2)李校长乘车从纵掉园去生态园,乘坐网约顺风车比乘坐网约出租车节省了2元.求从纵棹园去生态园的路程;
(3)网约专车为了和网约顺风车竞争客户,分别推出了优惠方式:网约顺风车对于乘车路程在5千米以上(含5千米)的客户每次收费立减6元;网约专车打车车费一律七五折优惠.对采用哪一种打车方式更合算提出你的建议.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,与y轴相交于点C,直线y=kx+n(k≠0)经过B,C两点,已知A(1,0),C(0,3),且BC=5.
(1)分别求直线BC和抛物线的解析式(关系式);
(2)在抛物线的对称轴上是否存在点P,使得以B,C,P三点为顶点的三角形是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
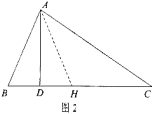
【题目】阅读下面材料:小明遇到这样一个问题:
如图1,在△ABC中,∠B=2∠C,AD⊥BC于点D,求证:BC=AB+2BD.
小明利用条件AD⊥BC,在CD上截取DH=BD,如图2,连接AH,既构造了等腰△ABH,又得到BH=2BD,从而命题得证。
(1)根据阅读材料,证明:BC=AB+2BD;
(2)参考小明的方法,解决下面的问题:
如图3,在△ABC中,∠BAC=90°,∠ABD=∠BCE,∠ABC=∠DCE,请探究AD与BE的数量关系,并说明理由。


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com