已知实数x，y满足x+y=2，且求k的值．

三位同学分别提出了以下三种不同的解题思路：

甲同学：先解关于x，y的方程组，再求k的值．

乙同学：先将方程组中的两个方程相加，再求k的值．

丙同学：先解方程组，再求k的值．

（2）你最欣赏（1）中的哪种思路？先根据你所选的思路解答此题，再对你选择的思路进行简要评价．

（评价参考建议：基于观察到题目的什么特征设计的相应思路，如何操作才能实现这些思路、运算的简洁性，以及你依此可以总结什么解题策略等等）

请先在以下相应方框内打勾，再解答相应题目．

【题目】从﹣4，﹣3，﹣2，﹣1，0，1，3，4，5这九个数中，随机抽取一个数，记为a，则数a使关于x的不等式组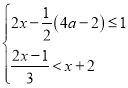至少有四个整数解，且关于x的分式方程＝1有非负整数解的概率是（　　）

A.B.C.D.

【题目】如图，已知二次函数y= x2+ x﹣ 的图象与x轴交于点 A，B，交 y 轴于点 C，抛物线的顶点为 D．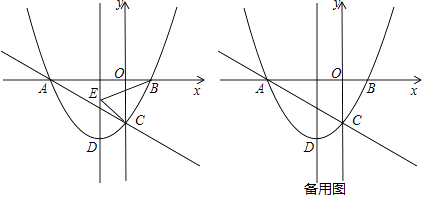

（1）求抛物线顶点 D 的坐标以及直线 AC 的函数表达式；
（2）点 P 是抛物线上一点，且点P在直线 AC 下方，点 E 在抛物线对称轴上，当△BCE 的周长最小时，求△PCE 面积的最大值以及此时点 P 的坐标；
（3）在（2）的条件下，过点 P 且平行于 AC 的直线分别交x轴于点 M，交 y 轴于点N，把抛物线y= x2+ x﹣ 沿对称轴上下平移，平移后抛物线的顶点为 D'，在平移的过程中，是否存在点 D'，使得点 D'，M，N 三点构成的三角形为直角三角形，若存在，直接写出点 D'的坐标；若不存在，请说明理由．

A. 0.5元、0.6元 B. 0.4元、0.5元 C. 0.3元、0.4元 D. 0.6元、0.7元

【题目】如图，点A，B分别在函数y＝（k1＞0）与函数y＝（k2＜0）的图象上，线段AB的中点M在x轴上，△AOB的面积为4，则k1﹣k2的值为（　　）

A.2B.4C.6D.8

【题目】如图，在△ABC中，AB=AC，点D是△ABC内一点，AD=BD，且AD⊥BD，连接CD．过点C作CE⊥BC交AD的延长线于点 E，连接BE．过点D作DF⊥CD交BC于点F．

（1）若BD=DE= ，CE= ，求BC的长；
（2）若BD=DE，求证：BF=CF．

【题目】对任意一个正整数m，如果m=k（k+1），其中k是正整数，则称m为“矩数”，k 为m的最佳拆分点．例如，56=7×（7+1），则56是一个“矩数”，7为56的最佳拆分点．
（1）求证：若“矩数”m是3的倍数，则m一定是6的倍数；
（2）把“矩数”p与“矩数”q的差记为 D（p，q），其中p＞q，D（p，q）＞0．例如，20=4×5，6=2×3，则 D（20，6）=20﹣6=14．若“矩数”p的最佳拆分点为t，“矩数”q的最佳拆分点为s，当 D（p，q）=30时，求 的最大值．

【题目】某电器超市销售每台进价分别为2000元、1700元的、两种型号的空调，如表是近两周的销售情况：

（1）求、两种型号的空调的销售单价；

（2）求近两周的销售利润．

（1）在图1中，∠AEC与∠EAB，∠ECD之间的关系是：________________．

（2）在图2中，∠AEC与∠EAB，∠ECD之间的关系是：________________．

（3）在图3中，∠AEC与∠EAB，∠ECD之间的关系是：________________．

（4）在图______中，求证：________________．（并写出完整的证明过程）

【题目】为加快5G网络建设，某移动通信公司在山顶上建了一座5G信号通信塔AB，山高BE＝100米（A，B，E在同一直线上），点C与点D分别在E的两侧（C，E，D在同一直线上），BE⊥CD，CD之间的距离1000米，点D处测得通信塔顶A的仰角是30°，点C处测得通信塔顶A的仰角是45°（如图），则通信塔AB的高度约为（　　）米．（参考数据：，）

A.350B.250C.200D.150