
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,平行四边形![]() 的边
的边![]() 在
在![]() 轴上,点
轴上,点![]() ,线段
,线段![]() ,线段
,线段![]() ,且
,且![]() ,
,![]() 与
与![]() 的交点记为
的交点记为![]() ,连接
,连接![]() .
.
(1)求![]() 的面积.
的面积.
(2)如图2,在线段![]() 上有两个动点
上有两个动点![]() 、
、![]() (
(![]() 在
在![]() 点上方),且
点上方),且![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 为线段
为线段![]() 上一动点,当
上一动点,当![]() 的值最小时,求出此时
的值最小时,求出此时![]() 点的坐标;
点的坐标;
(3)在(2)的条件下,在![]() 轴上找一点
轴上找一点![]() ,
,![]() 轴上找一点
轴上找一点![]() ,使得
,使得![]() 取得最小值,请求出
取得最小值,请求出![]() 的最小值.
的最小值.


查看答案和解析>>
科目: 来源: 题型:
【题目】如图,边长为4的等边三角形AOB的顶点O在坐标原点,点A在x轴的正半轴上,点B在第一象限.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段BP的中点绕点P按顺时针方向旋转60°得点C,点C随点P的运动而运动,连接CP、CA.过点P作PD⊥OB于D点
(1)直接写出BD的长并求出点C的坐标(用含t的代数式表示)
(2)在点P从O向A运动的过程中,△PCA能否成为直角三角形?若能,求t的值.若不能,请说明理由;
(3)点P从点O运动到点A时,点C运动路线的长是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】某服装公司招工广告承诺:熟练工人每月工资至少3000元.每天工作8小时,一个月工作25天.月工资底薪800元,另加计件工资.加工1件A型服装计酬16元,加工1件B型服装计酬12元.在工作中发现一名熟练工加工1件A型服装和2件B型服装需4小时,加工3件A型服装和1件B型服装需7小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读理解:
材料1:对于一个关于![]() 的二次三项式
的二次三项式![]() ,除了可以利用配方法求该多项式的取值范围外,爱思考的小川同学还想到了其他的方法;比如先令
,除了可以利用配方法求该多项式的取值范围外,爱思考的小川同学还想到了其他的方法;比如先令![]() ,然后移项可得:
,然后移项可得:![]() ,再利用一元二次方程根的判别式来确定
,再利用一元二次方程根的判别式来确定![]() 的取值范围,请仔细阅读下面的例子:
的取值范围,请仔细阅读下面的例子:
例:求![]() 的取值范围;
的取值范围;
解:令![]()
![]()
![]()
![]()
![]() ;
;
材料2:在学习完一元二次方程的解法后,爱思考的小川同学又想到仿造一元二次方程的解法来解决一元二次不等式的解集问题,他的具体做法如下:
若关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() 、
、![]() ,则关于
,则关于![]() 的一元二次不等式
的一元二次不等式![]() 的解集为:
的解集为:![]() 或
或![]() ;则关于
;则关于![]() 的一元二次不等式的
的一元二次不等式的![]() 的解集为:
的解集为:![]() .
.
材料3:若关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() 、
、![]() ;则
;则![]() ;
;![]() ,我们称之为韦达定理;
,我们称之为韦达定理;
请根据上述材料,解答下列问题:
(1)若关于![]() 的二次三项式
的二次三项式![]() (
(![]() 为常数)的最小值为
为常数)的最小值为![]() ,则
,则![]() ________.
________.
(2)求出代数式![]() 的取值范围.
的取值范围.
(3)若关于![]() 的代数式
的代数式![]() (其中
(其中![]() 、
、![]() 为常数,且
为常数,且![]() )的最小值为
)的最小值为![]() ,最大值为4,请求出满足条件的
,最大值为4,请求出满足条件的![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形![]() 中,对角线
中,对角线![]() ,
,![]() 相较于点
相较于点![]() ,以
,以![]() 为边向外作等边
为边向外作等边![]() ,连接
,连接![]() ,交
,交![]() 于
于![]() .
.
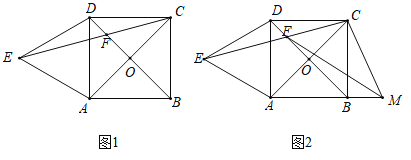
(1)如图1,若![]() ,求
,求![]() 的长
的长
(2)如图2,点![]() 为
为![]() 的延长线上一点,连接
的延长线上一点,连接![]() ,连接
,连接![]() 且
且![]() 平分
平分![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在“绿满重庆”行动中,江北区种植了大量的小叶榕和银杏树,根据林业专家的分析,树叶在进行光合作用后产生的分泌物能在空气中吸附悬浮颗粒,这样就达到了滞尘净化空气的作用.
(1)若某小区今年要种植银杏树和小叶榕共450株,且银杏树的数量不超过小叶榕数量的2倍,求今年该小区小叶榕至少种植多少株?
(2)已知每一片银杏树叶一年平均滞尘量为![]() ,一株银杏树去年有3500片树叶,冬季树叶全部掉落后,今年新长出了树叶,且这株银杏今年的滞尘量是去年滞尘量的1.1倍还多
,一株银杏树去年有3500片树叶,冬季树叶全部掉落后,今年新长出了树叶,且这株银杏今年的滞尘量是去年滞尘量的1.1倍还多![]() .已知每片小叶榕树叶的滞尘量比银杏树叶多
.已知每片小叶榕树叶的滞尘量比银杏树叶多![]() ,一株小叶榕今年的树叶总量比今年的这株银杏要少
,一株小叶榕今年的树叶总量比今年的这株银杏要少![]() ,明年这株小叶榕树叶将在今年的基础上掉落
,明年这株小叶榕树叶将在今年的基础上掉落![]() ,但又会新长出1000片树叶,若今明两年这株小叶榕共滞尘量为
,但又会新长出1000片树叶,若今明两年这株小叶榕共滞尘量为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
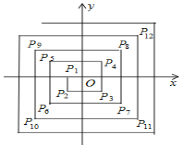
【题目】如图,在平面直角坐标系中,从点P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次扩展下去,则P2020的坐标为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,小彬和爸爸一起去车站接从外地学习回来的妈妈,在去的过程中,小彬坐在汽车上看着时速表,用所学知识绘制了一张反映小车速度与时间的关系图,请你根据图象回答以下问题:

(1)在上述过程中,自变量是什么?因变量是什么?
(2)小车共行驶了多少时间?最高时速是多少?
(3)汽车在哪段时间保持匀速运动?速度是多少?
(4)汽车在哪段时间内速度在增加?哪段时间内速度在减少?
查看答案和解析>>
科目: 来源: 题型:
【题目】推理填空.如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD,理由如下:
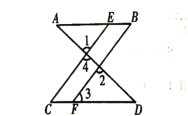
解:因为∠1=∠2(已知),且∠1=∠4( )
所以∠2=∠4(等量代换)
所以CE∥BF( )
所以∠ =∠3( )
又因为∠B=∠C(已知),所以∠3=∠B( )
所以AB∥CD ( )
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知A是双曲线y= ![]() (k>0)在第一象限内的一点,O为坐标原点,直线OA交双曲线于另一点C,当OA在第一象限的角平分线上时,将OA向上平移
(k>0)在第一象限内的一点,O为坐标原点,直线OA交双曲线于另一点C,当OA在第一象限的角平分线上时,将OA向上平移 ![]() 个单位后,与双曲线在第一象限交于点M,交y轴于点N,若
个单位后,与双曲线在第一象限交于点M,交y轴于点N,若 ![]() =2,
=2,
(1)求直线MN的解析式;
(2)求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com