
科目: 来源: 题型:
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,将△APB绕点B逆时针旋转一定角度后,可得到△CQB. 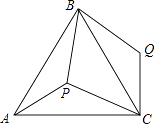
(1)求点P与点Q之间的距离;
(2)求∠APB的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(m+1)x+ ![]() (m2+1)=0有实数根.
(m2+1)=0有实数根.
(1)求m的值;
(2)先作y=x2﹣(m+1)x+ ![]() (m2+1)的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
(m2+1)的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求n2﹣4n的最大值和最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,A(﹣3,2),B(﹣1,﹣2),C(1,﹣1).将△ABC向右平移3个单位长度,然后再向上平移1个单位长度,可以得到△A1B1C1.
(1)△A1B1C1的顶点A1的坐标为 ;顶点C1的坐标为 .
(2)求△A1B1C1的面积.
(3)已知点P在x轴上,以A1、C1、P为顶点的三角形面积为![]() ,则P点的坐标为 .
,则P点的坐标为 .

查看答案和解析>>
科目: 来源: 题型:
【题目】在下列网格图中,每个小正方形的边长均为![]() 个单位长度.已知
个单位长度.已知![]() 在网格图中的位置如图所示.
在网格图中的位置如图所示.
(1)请在网格图中画出![]() 向右平移
向右平移![]() 单位后的图形
单位后的图形![]() ,并直接写出平移过程中线段
,并直接写出平移过程中线段![]() 扫过的面积;
扫过的面积;
(2)请在网格图中画出![]() 以
以![]() 为对称中心的图形
为对称中心的图形![]() .(保留作图痕迹)
.(保留作图痕迹)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点F在线段AB上,点E、G在线段CD上,AB∥CD.
(1)若BC平分∠ABD,∠D=100°,求∠ABC的度数.
解:∵AB∥CD(已知),
∴∠ABD+∠D=180°,( )
∵∠D=100°,(已知)
∴∠ABD= °,
∵BC平分∠ABD,(已知)
∴∠ABC=![]() ∠ABD=40°.(角平分线的定义)
∠ABD=40°.(角平分线的定义)
(2)若∠1=∠2,求证:AE∥FG.
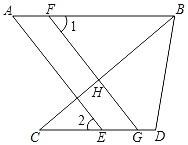
查看答案和解析>>
科目: 来源: 题型:
【题目】按要求作图.(不写作法,保留作图痕迹)

(1)如图1,点A在∠O的一边上,在图1中完成:
①过点A画直线AB⊥OA,与∠O的另一边相交于点B;
②过点B画直线BC∥OA;
(2)如图2,△ABC是钝角三角形,在图2中完成:
①画△ABC的中线AD;
②画△ABC的角平分线BE;
③画△ABC的高线CF.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,将
,将![]() 对折,使点
对折,使点![]() 的对称点
的对称点![]() 落在直线
落在直线![]() 上,折痕交
上,折痕交![]() 轴于点
轴于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)若已知第四象限内的点![]() ,在直线
,在直线![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() 为平行四边形?若存在,求出点
为平行四边形?若存在,求出点![]() 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(3)设经过点![]() 且与
且与![]() 轴垂直的直线与直线
轴垂直的直线与直线![]() 的交点为
的交点为![]() 为线段
为线段![]() 上一点,求
上一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
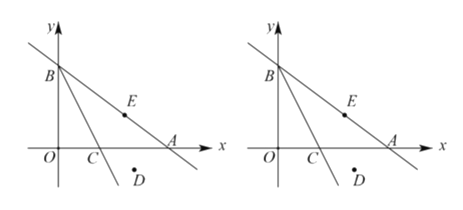
【题目】如图,以OA为边的△OAB面积为2,其中点B的横、纵坐标均不超过4,且都不小于0,在下列叙述中,正确的是:_____.(请写出所有正确的选项)
①若点B的横坐标是4,则满足条件的点B有且只有1个;
②若点B是整点(即横、纵坐标都是整数),则满足条件的点B有4个;
③在坐标系内,对于任意满足题意的点B,一定存在一点C,使得△CAB、△COA、△COB面积相等;
④在坐标系内,存在一个定点D,使得对于任意满足条件的点B,△DBA、△DBO面积相等.

查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.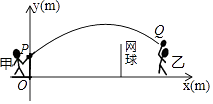
(1)当a=﹣ ![]() 时,①求h的值;
时,①求h的值;
②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为 ![]() m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com