
科目: 来源: 题型:
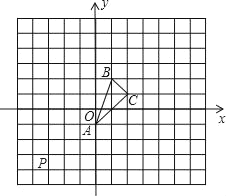
【题目】如图是网格图,每个小正方形的边长均为1.△ABC它在坐标平面内平移,得到△PEF,点A平移后落在点P的位置上.
(1)请你在图中画出△PEF,并写出顶点P、E、F的坐标;
(2)说出△PEF是由△ABC分别经过怎样的平移得到的?
查看答案和解析>>
科目: 来源: 题型:
【题目】问题探究:
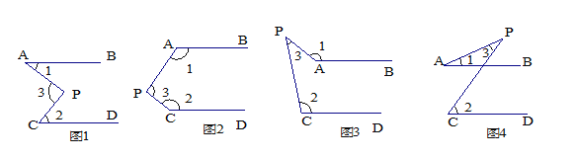
如下面四个图形中, AB∥CD.
(1)分别说出图1、图2、图3、图4中,∠1与∠2、∠3三者之间的关系.
(2)请你从中任选一个加以说明理由.
解决问题:
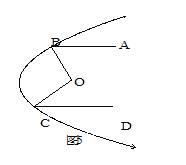
(3)如图5所示的是一探照灯灯碗的纵剖面,从位于O点的灯泡发出两束光线OB、OC经灯碗反射后平行射出.如果∠ABO=57°,∠DCO=44°,那么∠BOC=_______°.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一元二次方程1﹣(x﹣3)(x+2)=0,有两个实数根x1和x2 , (x1<x2),则下列判断正确的是( )
A.﹣2<x1<x2<3
B.x1<﹣2<3<x2
C.﹣2<x1<3<x2
D.x1<﹣2<x2<3
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列解方程组的方法,回答问题.
解方程组![]()
解:由①﹣②得2x+2y=2即x+y=1③
③×16得16x+16y=16④
②﹣④得x=﹣1,从而可得y=2
∴原方程组的解是![]()
(1)请你仿照上面的解法解方程组![]() ;
;
(2)请大胆猜测关于x、y的方程组![]()
的解是什么?并利用方程组的解加以验证.
查看答案和解析>>
科目: 来源: 题型:
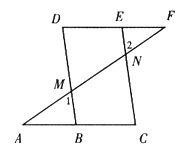
【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解: ∵EF∥AD,
∴∠2=____(____________________________)
又∵∠1=∠2
∴∠1=∠3(等量代换)
∵AB∥_____(_____________________________)
∴∠BAC+______=180°(___________________________)
∵∠BAC=70°
∴∠AGD=_______.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D在边AC上,且BD=DA=BC.
(1)如图1,填空:∠A=_______.
(2)如图2,若M为线段AC上的点,过M作直线MH⊥BD于H,分别交直线AB、BC于点N、E.
①求证:△BNE是等腰三角形;
②试写出线段AN、CE、CD之间的数量关系,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图在平面直角坐标系中,A.B两点的坐标分别为(﹣2,2),(1,8),
(1)求△ABO的面积.
(2)若y轴上有一点M,且△MAB的面积为10.求M点的坐标.
(3)如图,把直线AB以每秒2个单位的速度向右平移,运动t秒钟后,直线AB过点F(0,﹣2),此时A点的坐标为 ,B点的坐标为 ,过点A作AE⊥y轴于点E,过点B作BD⊥y轴于点D,请根据S△FBD=S△FAE+S梯形ABDE,求出满足条件的运动时间t的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,∠1=∠2,∠C=∠D。
求证:∠A=∠F。
证明:∵∠1=∠2(已知),
又∠1=∠DMN(_______________),
∴∠2=∠_________(等量代换),
∴DB∥EC( ),
∴∠DBC+∠C=1800(两直线平行 , ),
∵∠C=∠D( ),
∴∠DBC+ =1800(等量代换),
∴DF∥AC( ,两直线平行),
∴∠A=∠F( )
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,王大伯家屋后有一块长12m、宽8m的长方形空地,他在以较长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长最长不超过( )
A.3m
B.4m
C.5m
D.6m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com